2.2 — Random Variables & Distributions

ECON 480 • Econometrics • Fall 2022

Dr. Ryan Safner
Associate Professor of Economics

safner@hood.edu
ryansafner/metricsF22
metricsF22.classes.ryansafner.com

Contents

Random Variables

Discrete Random Variables

Expected Value and Variance

Continuous Random Variables

The Normal Distribution

Random Variables

Experiments

  • An experiment is any procedure that can (in principle) be repeated infinitely and has a well-defined set of outcomes

Example

Flip a coin 10 times.

Random Variables

  • A random variable (RV) takes on values that are unknown in advance, but determined by an experiment

  • A numerical summary of a random outcome

Example

The number of heads from 10 coin flips

Random Variables: Notation

  • Random variable \(X\) takes on individual values \((x_i)\) from a set of possible values

  • Often capital letters to denote RV’s

    • lowercase letters for individual values

Example

Let \(X\) be the number of Heads from 10 coin flips. \(\quad x_i \in \{0, 1, 2,...,10\}\)

Discrete Random Variables

Discrete Random Variables

  • A discrete random variable: takes on a finite/countable set of possible values

Example

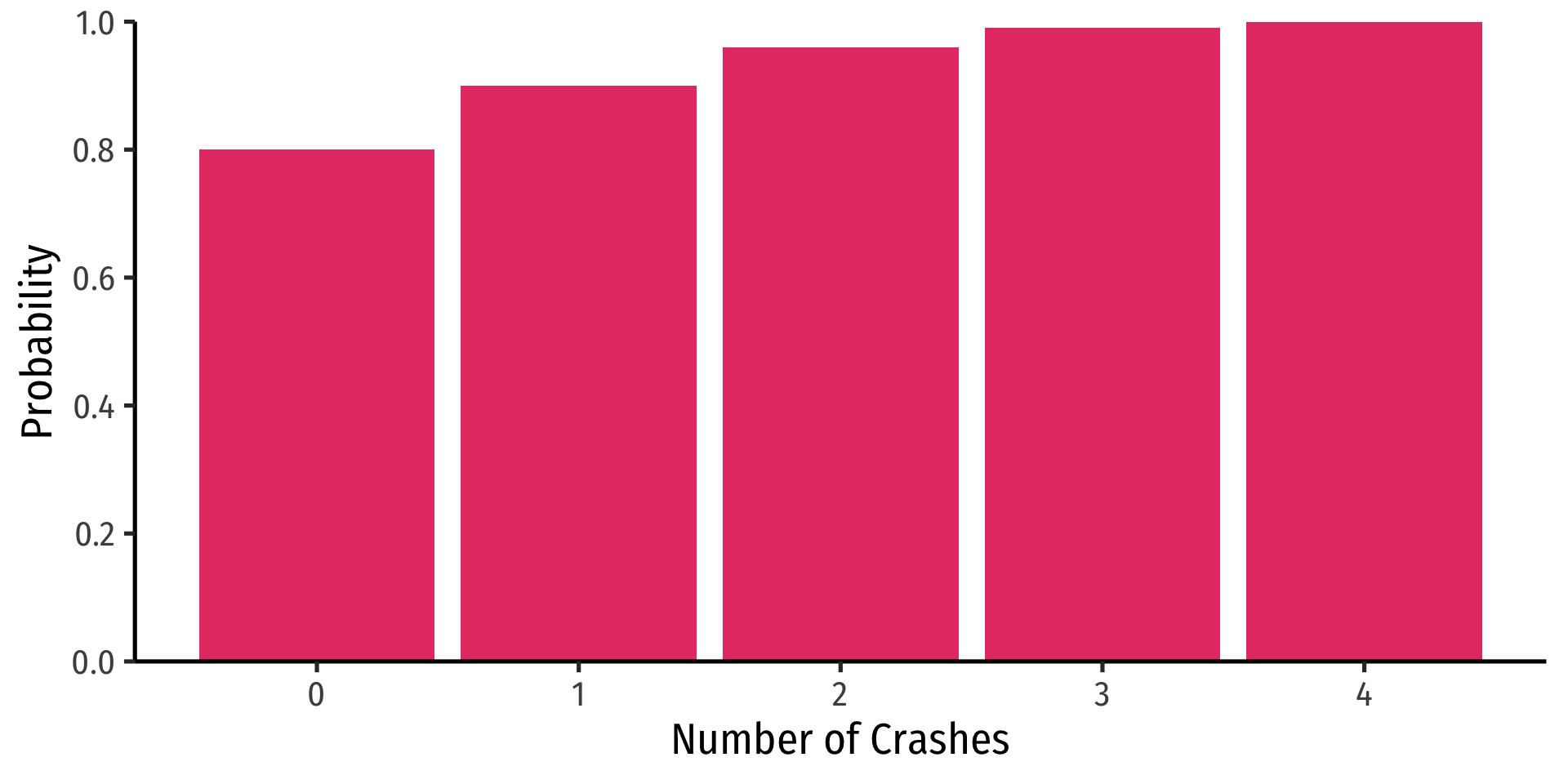
Let \(X\) be the number of times your computer crashes this semester1, \(x_i \in \{0, 1, 2, 3, 4\}\)

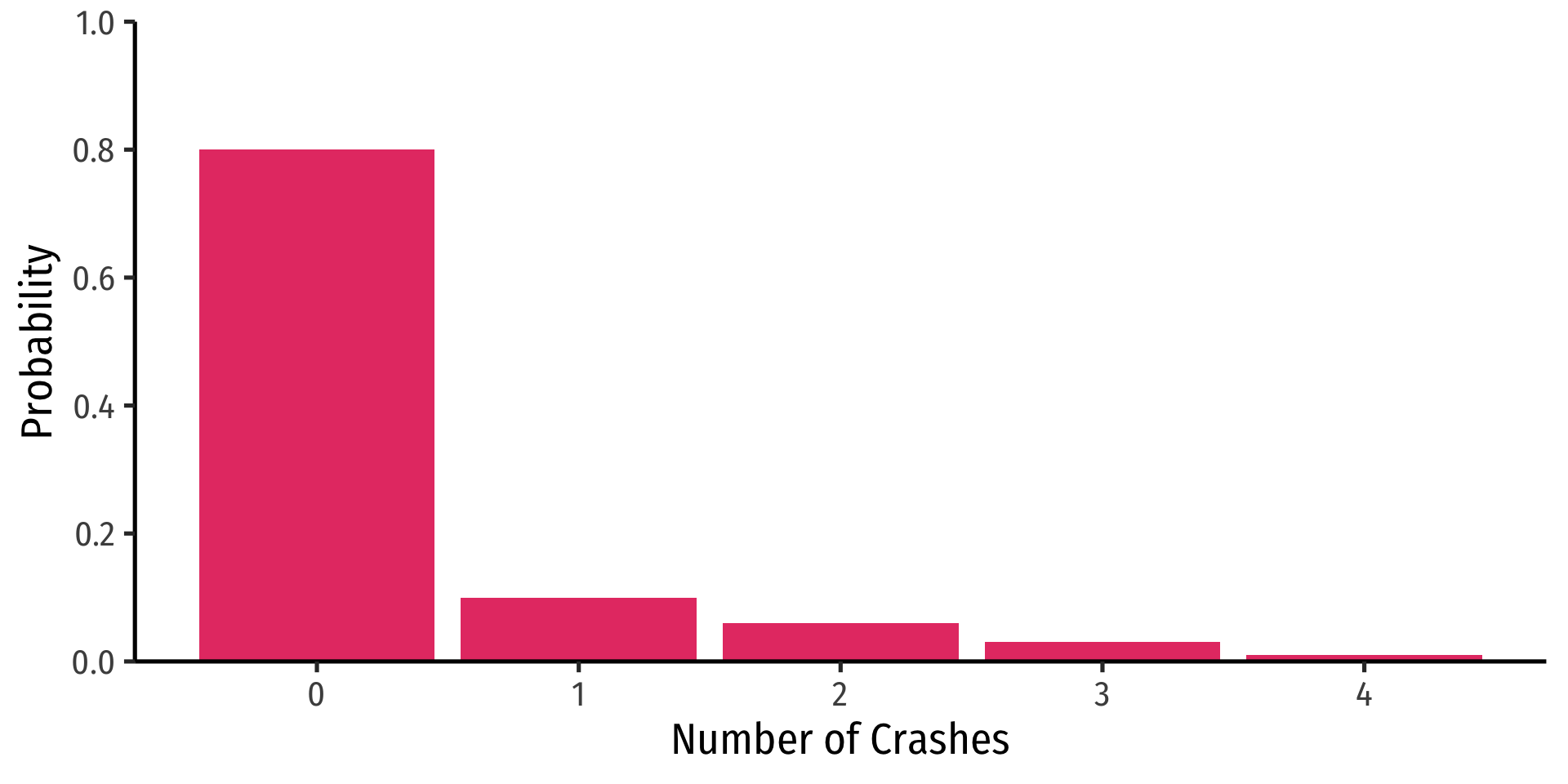
Discrete Random Variables: Probability Distribution

  • Probability distribution of a R.V. fully lists all the possible values of \(X\) and their associated probabilities
\(x_i\) \(P(X=x_i)\)
0 0.80
1 0.10
2 0.06
3 0.03
4 0.01

Discrete Random Variables: pdf

  • Probability distribution function (pdf) summarizes the possible outcomes of \(X\) and their probabilities

  • Notation: \(f_X\) is the pdf of \(X\):

\[f_X=p_i, \quad i=1,2,...,k\]

  • For any real number \(x_i\), \(f(x_i)\) is the probablity that \(X=x_i\)
\(x_i\) \(P(X=x_i)\)
0 0.80
1 0.10
2 0.06
3 0.03
4 0.01
  • What is \(f(0)\)?
  • What is \(f(3)\)?

Discrete Random Variables: pdf Graph

crashes<-tibble(number = c(0,1,2,3,4),
                prob = c(0.80, 0.10, 0.06, 0.03, 0.01))

ggplot(data = crashes) +
  aes(x = number,
      y = prob)+
  geom_col(fill = "#e64173") +
  labs(x = "Number of Crashes",
       y = "Probability") +
  scale_y_continuous(breaks = seq(0,1,0.2),
                     limits = c(0,1),
                     expand = c(0,0))+
  theme_classic(base_family = "Fira Sans Condensed",
                base_size = 20)

Discrete Random Variables: cdf

  • Cumulative distribution function (cdf) lists probability \(X\) will be at most (less than or equal to) a given value \(x_i\)

  • Notation: \(F_X=P(X \leq x_i)\)

\(x_i\) \(f(x)\) \(F(x)\)
0 0.80 0.80
1 0.10 0.90
2 0.06 0.96
3 0.03 0.99
4 0.01 1.00
  • What is the probability your computer will crash at most once, \(F(1)\)?
  • What about three times, \(F(3)\)?

Discrete Random Variables: cdf Graph

crashes <- crashes %>%
  mutate(cum_prob = cumsum(prob))

crashes
# A tibble: 5 × 3
  number  prob cum_prob
   <dbl> <dbl>    <dbl>
1      0  0.8      0.8 
2      1  0.1      0.9 
3      2  0.06     0.96
4      3  0.03     0.99
5      4  0.01     1

Discrete Random Variables: cdf Graph

ggplot(data = crashes) +
  aes(x = number,
      y = cum_prob) +
  geom_col(fill="#e64173") +
  labs(x = "Number of Crashes",
       y = "Probability") +
  scale_y_continuous(breaks = seq(0,1,0.2),
                     limits = c(0,1),
                     expand = c(0,0)) +
  theme_classic(base_family = "Fira Sans Condensed",
                base_size = 20)

Expected Value and Variance

Expected Value of a Random Variable

  • Expected value of a random variable \(X\), written \(\mathbb{E}(X)\) (and sometimes \(\mu)\), is the long-run average value of \(X\) “expected” after many repetitions

\[\mathbb{E}(X)=\sum^k_{i=1} p_i x_i\]

  • \(\mathbb{E}(X)=p_1x_1+p_2x_2+ \cdots +p_kx_k\)

  • A probability-weighted average of \(X\), with each \(x_i\) weighted by its associated probability \(p_i\)

  • Also called the “mean” or “expectation” of \(X\), always denoted either \(\mathbb{E}(X)\) or \(\mu_X\)

Expected Value: Example I

Example

Suppose you lend your friend $100 at 10% interest. If the loan is repaid, you receive $110. You estimate that your friend is 99% likely to repay, but there is a default risk of 1% where you get nothing. What is the expected value of repayment?

Expected Value: Example II

Example

Let \(X\) be a random variable that is described by the following pdf:

\(x_i\) \(P(X=x_i)\)
1 0.50
2 0.25
3 0.15
4 0.10

Calculate \(\mathbb{E}(X)\).

The Steps to Calculate E(X), Coded

# Make a Random Variable called X
X <- tibble(x_i = c(1,2,3,4), # values of X
            p_i = c(0.50,0.25,0.15,0.10)) # probabilities


# Look at tibble
X
# A tibble: 4 × 2
    x_i   p_i
  <dbl> <dbl>
1     1  0.5 
2     2  0.25
3     3  0.15
4     4  0.1 


# Get expected value
X %>%
  summarize(expected_value = sum(x_i * p_i))
# A tibble: 1 × 1
  expected_value
           <dbl>
1           1.85

Variance of a Random Variable

  • The variance of a random variable \(X\), denoted \(var(X)\) or \(\sigma^2_X\) is:

\[\begin{align*}\sigma^2_X &= \mathbb{E}[(x_i-\mu_X)^2]\\ &=\sum_{i=1}^n(x_i-\mu_X)^2p_i\\ \end{align*}\]

  • This is the expected value of the squared deviations from the mean
    • i.e. the probability-weighted average of the squared deviations

Standard Deviation of a Random Variable

  • The standard deviation of a random variable \(X\), denoted \(sd(X)\) or \(\sigma_X\) is:

\[\sigma_X=\sqrt{\sigma_X^2}\]

  • This is the average or expected deviation from the mean

Standard Deviation: Example I

Example

What is the standard deviation of computer crashes?

\(x_i\) \(P(X=x_i)\)
0 0.80
1 0.10
2 0.06
3 0.03
4 0.01

The Steps to Calculate sd(X), Coded I

# get the expected value 
crashes %>%
  summarize(expected_value = sum(number*prob))
# A tibble: 1 × 1
  expected_value
           <dbl>
1           0.35


# save this for quick use
exp_value <- 0.35


crashes_2 <- crashes %>%
  select(-cum_prob) %>% # we don't need the cdf
  # create new columns
  mutate(deviations = number - exp_value, # deviations from exp_value
         deviations_sq = deviations^2, # square deviations
         weighted_devs_sq = prob * deviations_sq) # weight squared deviations by probability

The Steps to Calculate sd(X), Coded II

# look at what we made
crashes_2
# A tibble: 5 × 5
  number  prob deviations deviations_sq weighted_devs_sq
   <dbl> <dbl>      <dbl>         <dbl>            <dbl>
1      0  0.8       -0.35         0.122           0.098 
2      1  0.1        0.65         0.423           0.0423
3      2  0.06       1.65         2.72            0.163 
4      3  0.03       2.65         7.02            0.211 
5      4  0.01       3.65        13.3             0.133

The Steps to Calculate sd(X), Coded III

# now we want to take the expected value of the squared deviations to get variance
crashes_2 %>%
  summarize(variance = sum(weighted_devs_sq), # variance
            sd = sqrt(variance)) # sd is square root of variance
# A tibble: 1 × 2
  variance    sd
     <dbl> <dbl>
1    0.648 0.805

Standard Deviation: Example II

Example

What is the standard deviation of the random variable we saw before?

\(x_i\) \(P(X=x_i)\)
1 0.50
2 0.25
3 0.15
4 0.10

Hint: you already found it’s expected value.

Continuous Random Variables

Continuous Random Variables

  • Continuous random variables can take on an uncountable (infinite) number of values

  • So many values that the probability of any specific value is infinitely small:

\[P(X=x_i)\rightarrow 0\]

  • Instead, we focus on a range of values it might take on

Continuous Random Variables: pdf I

  • Probability density function (pdf) of a continuous variable represents the probability between two values as the area under a curve

  • The total area under the curve is 1

  • Since \(P(a)=0\) and \(P(b)=0\), \(P(a<X<b)=P(a \leq X \leq b)\)

  • See today’s appendix for how to graph math/stats functions in ggplot!

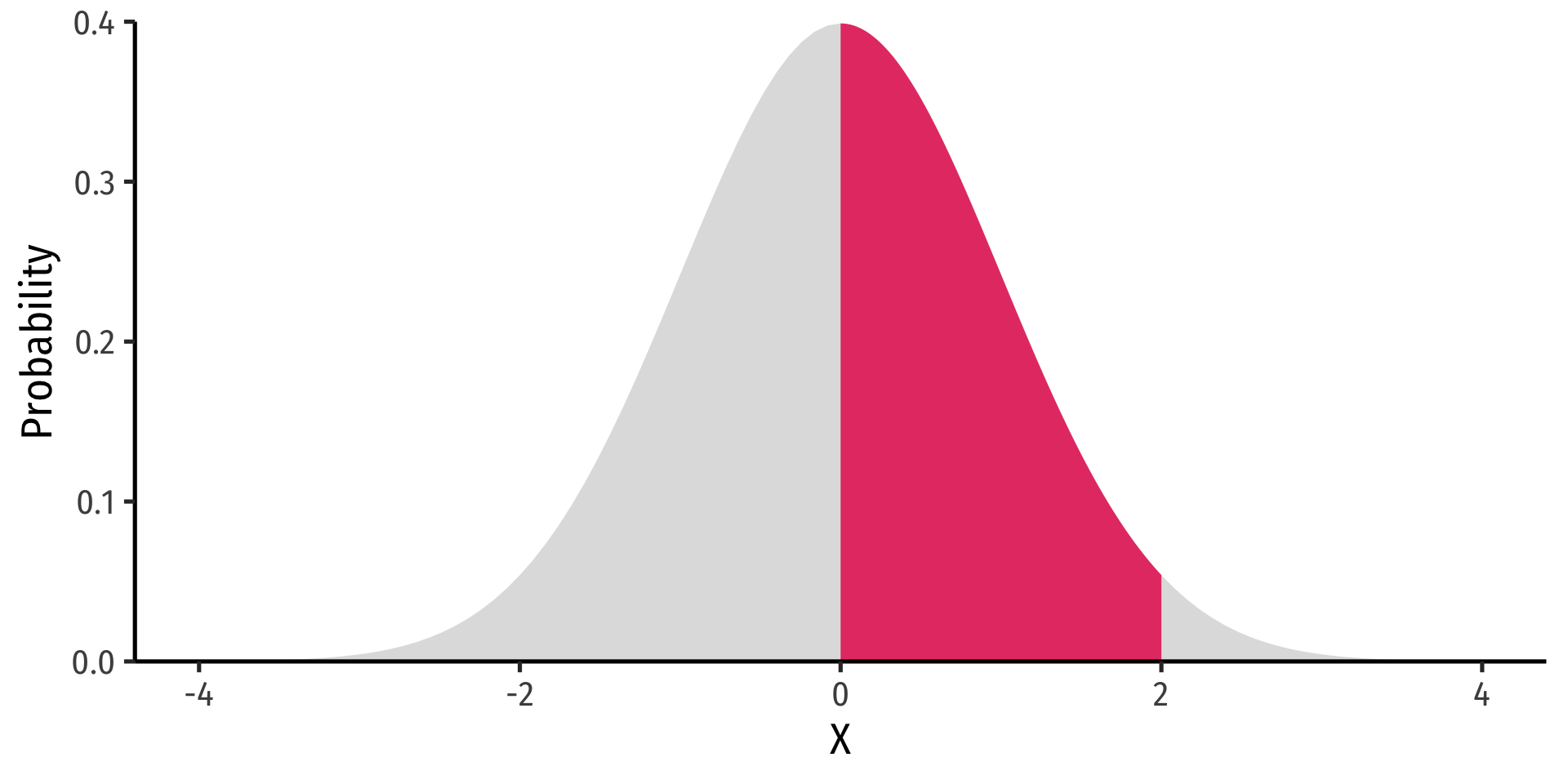
Example

\(P(0 \leq X \leq 2)\)

Continuous Random Variables: pdf II

  • FYI using calculus:

\[P(a \leq X \leq b) = \int_a^b f(x) dx \]

  • Complicated: software or (old fashioned!) probability tables to calculate

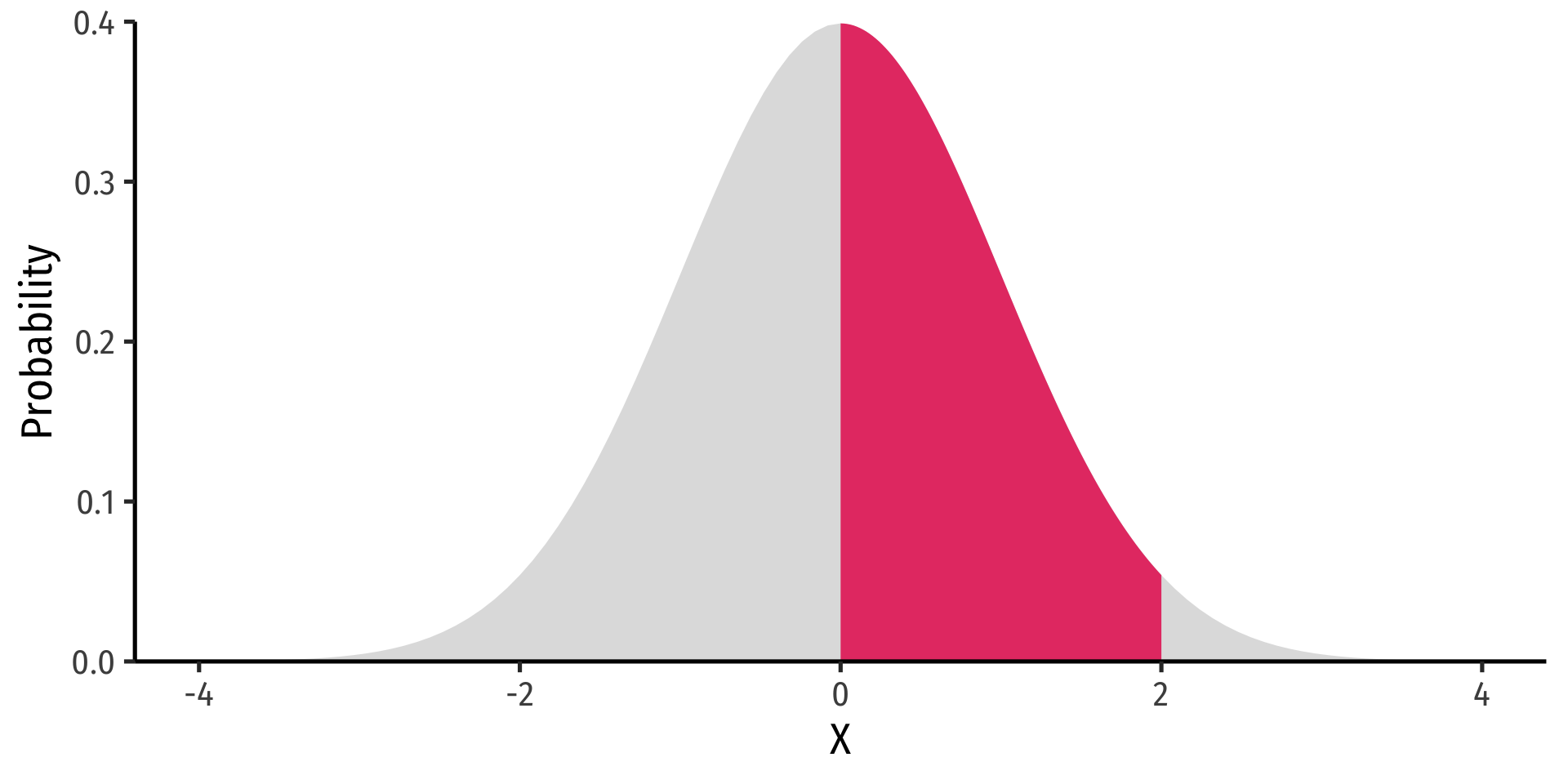
Example

\(P(0 \leq X \leq 2)\)

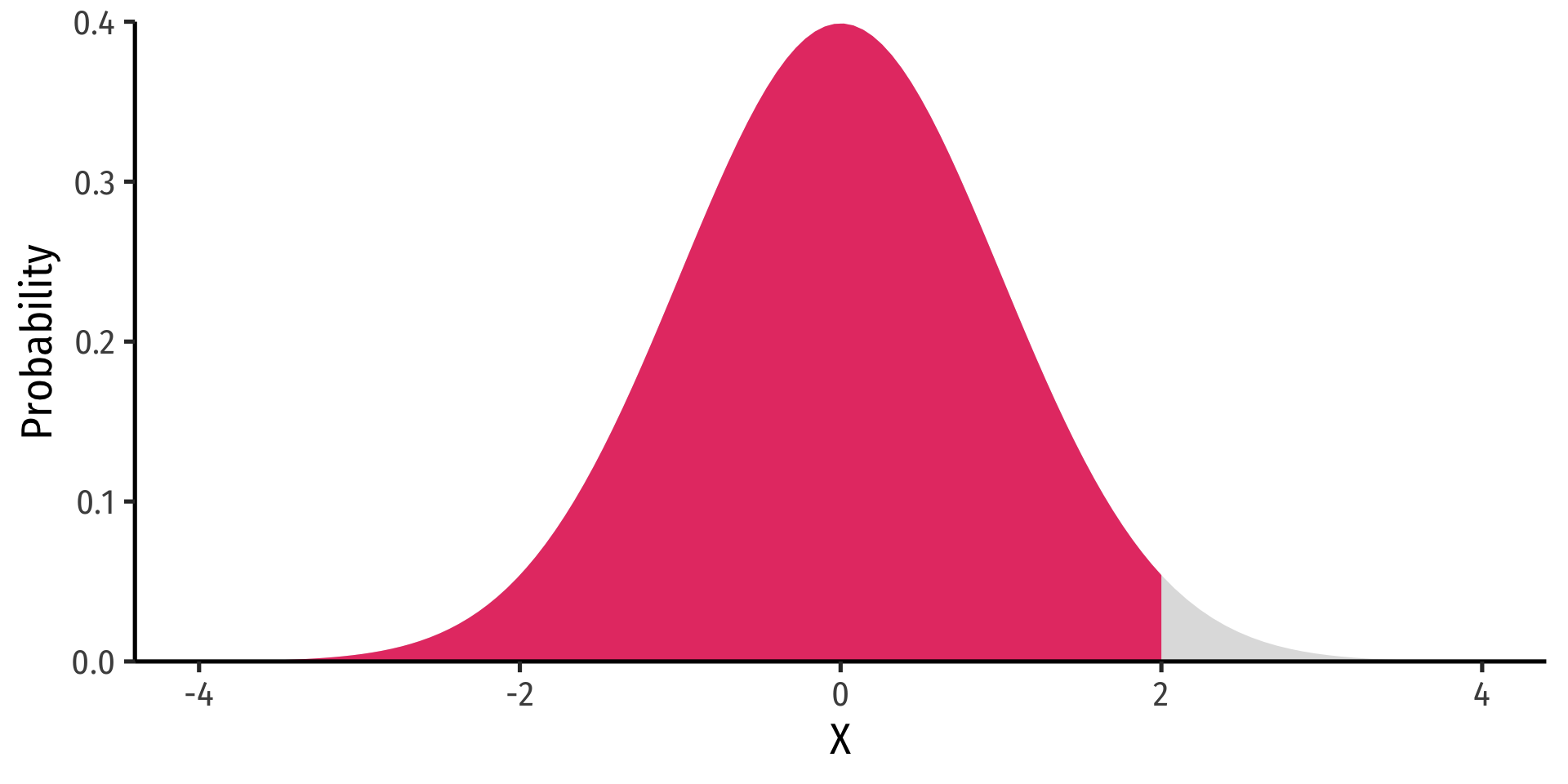
Continuous Random Variables: cdf I

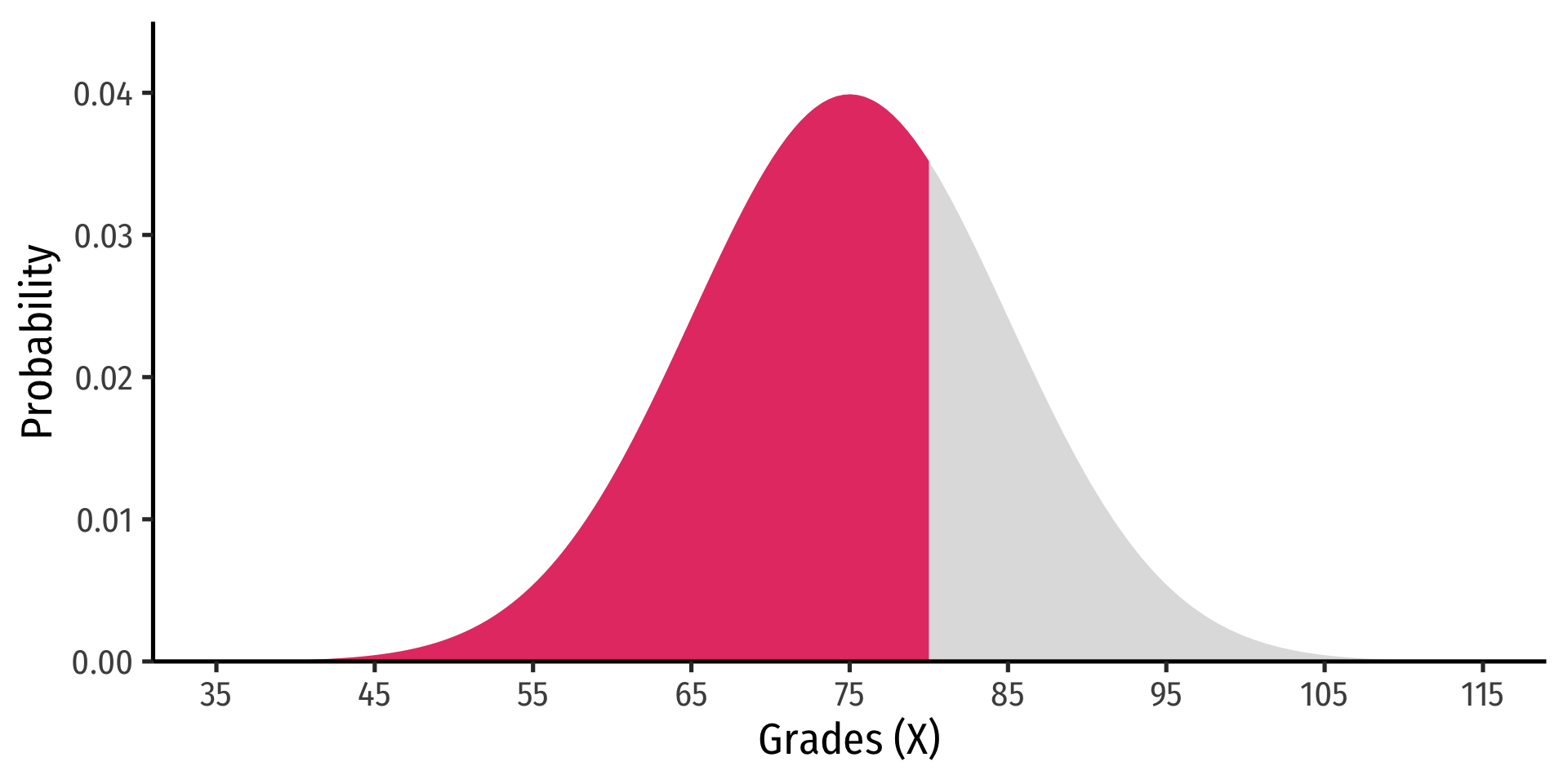
  • The cumulative density function (cdf) describes the area under the pdf for all values less than or equal to (i.e. to the left of) a given value, \(k\)

\[P(X \leq k)\]

Example

\(P(X \leq 2)\)

Continuous Random Variables: cdf II

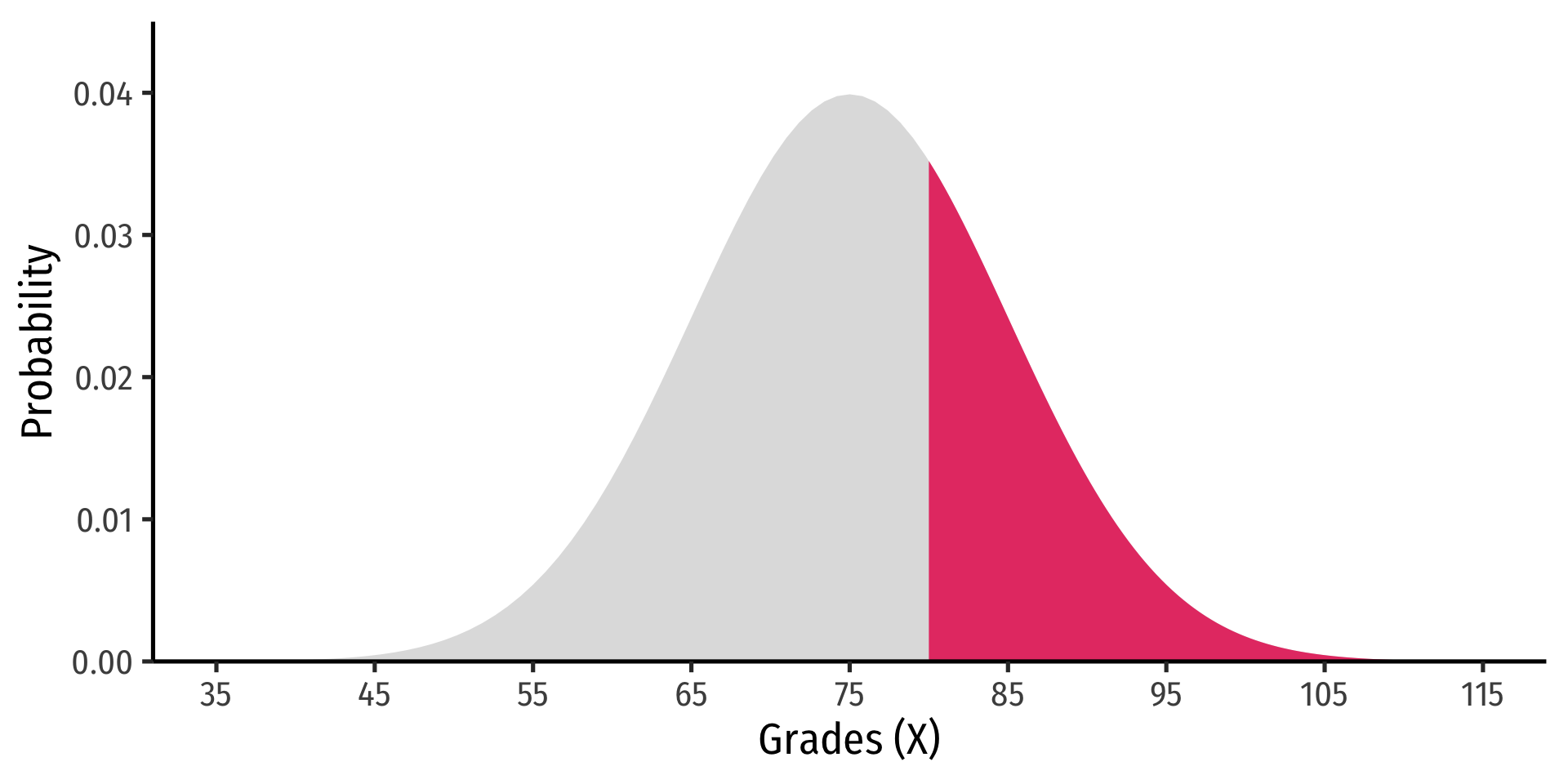
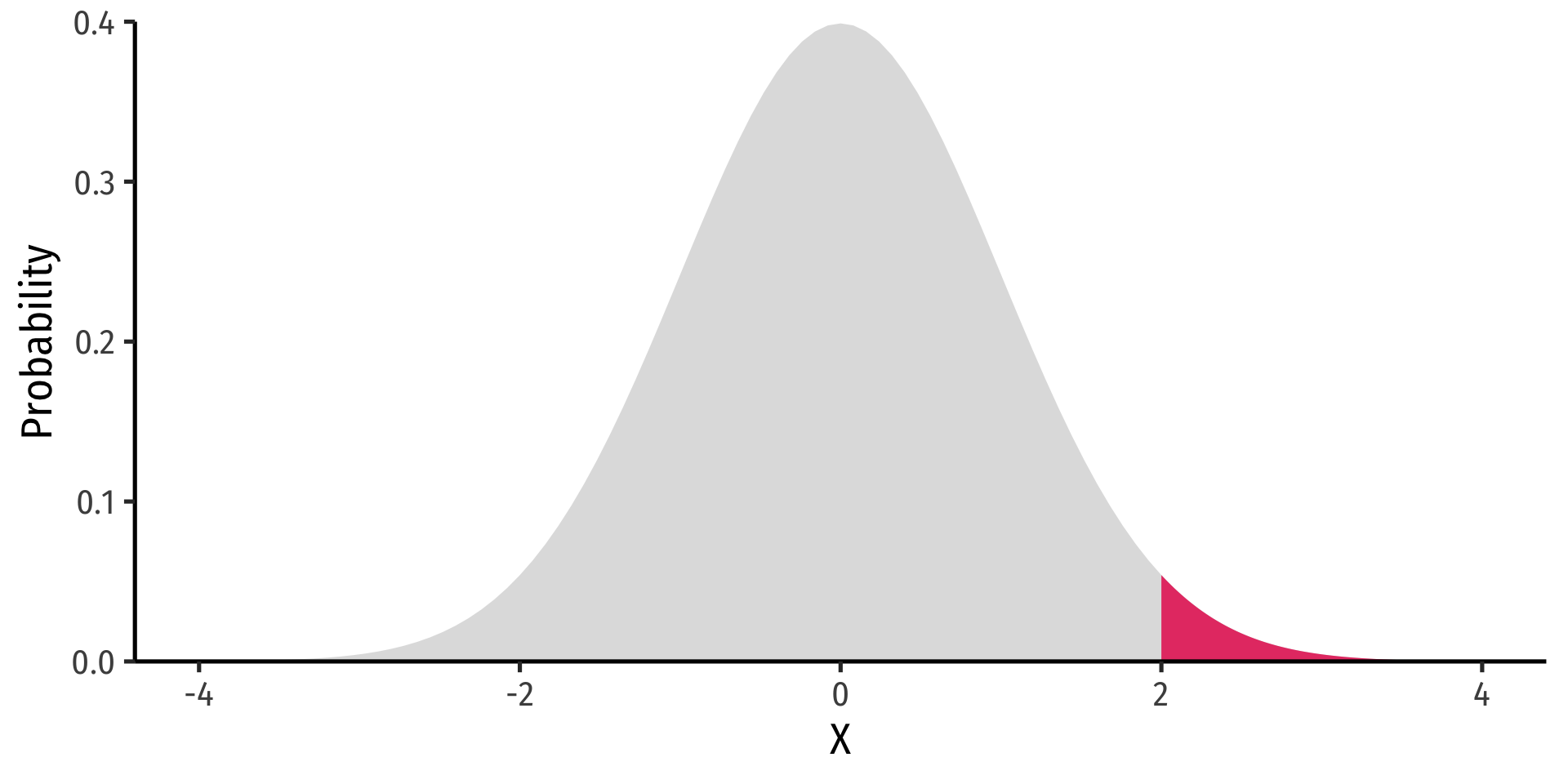
  • Note: to find probability of values greater than or equal to (to the right of) a given value \(k\):

\[P(X \geq k)=1-P(X \leq k)\]

Example

\(P(X \geq 2) = 1 - P(X \leq 2)\)

\(P(X \geq 2)=\) area under the pdf curve to the right of 2

The Normal Distribution

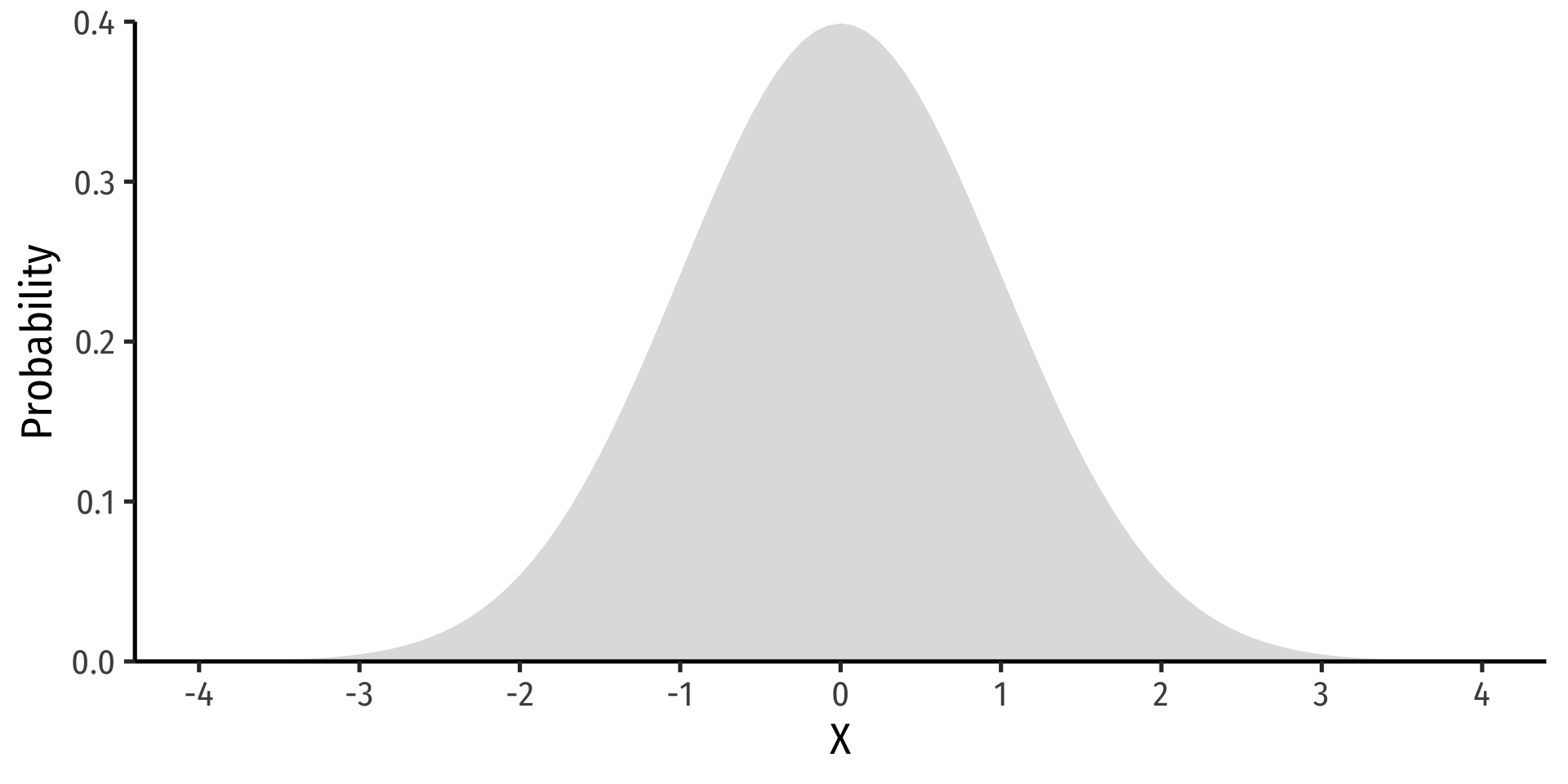
The Normal Distribution

  • The Gaussian or normal distribution is the most useful type of probability distribution

\[ X \sim N(\mu,\sigma)\]

  • “\(X\) is distributed Normally with mean \(\mu\) and standard deviation \(\sigma\)”

  • Continuous, symmetric, unimodal

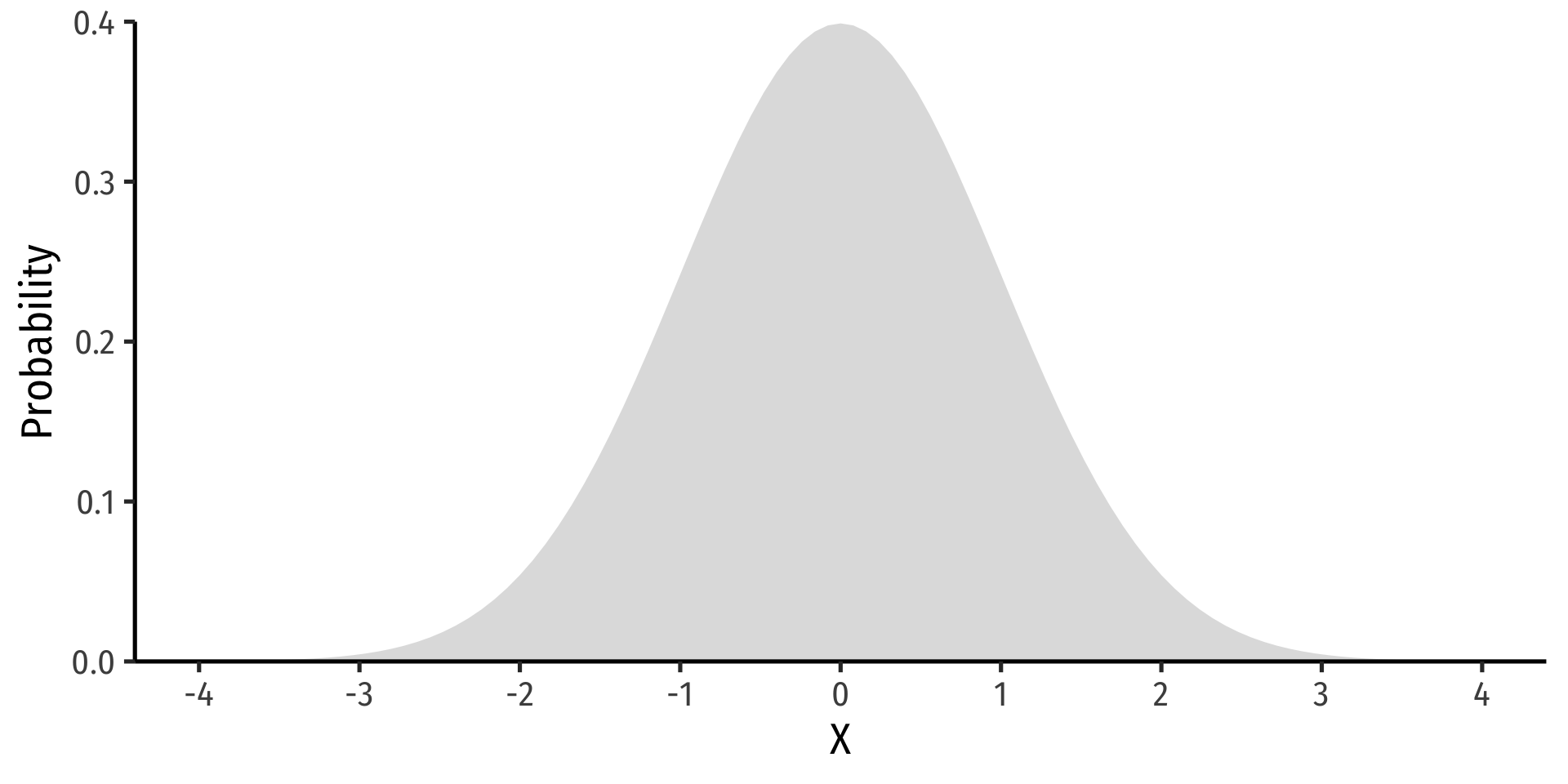
The Normal Distribution: pdf

  • FYI: The pdf of \(X \sim N(\mu, \sigma)\) is

\[P(X=k)= \frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{1}{2}\big(\frac{(k-\mu)}{\sigma}\big)^2}\]

  • Do not try and learn this, we have software and (previously tables) to calculate pdfs and cdfs

The Standard Normal Distribution

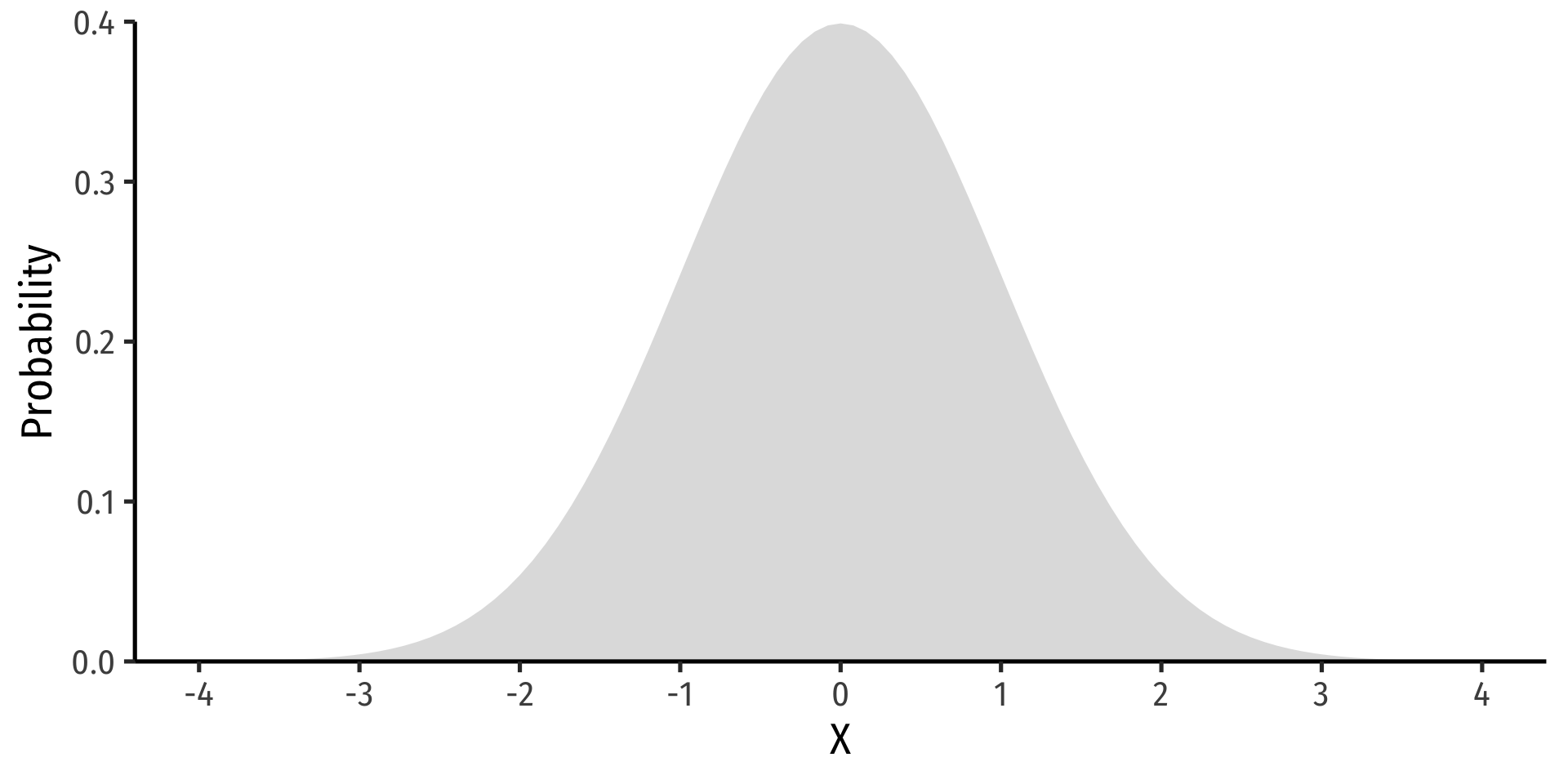
  • The standard normal distribution (often referred to as \(Z\)) has mean 0 and standard deviation 1

\[Z \sim N(0,1)\]

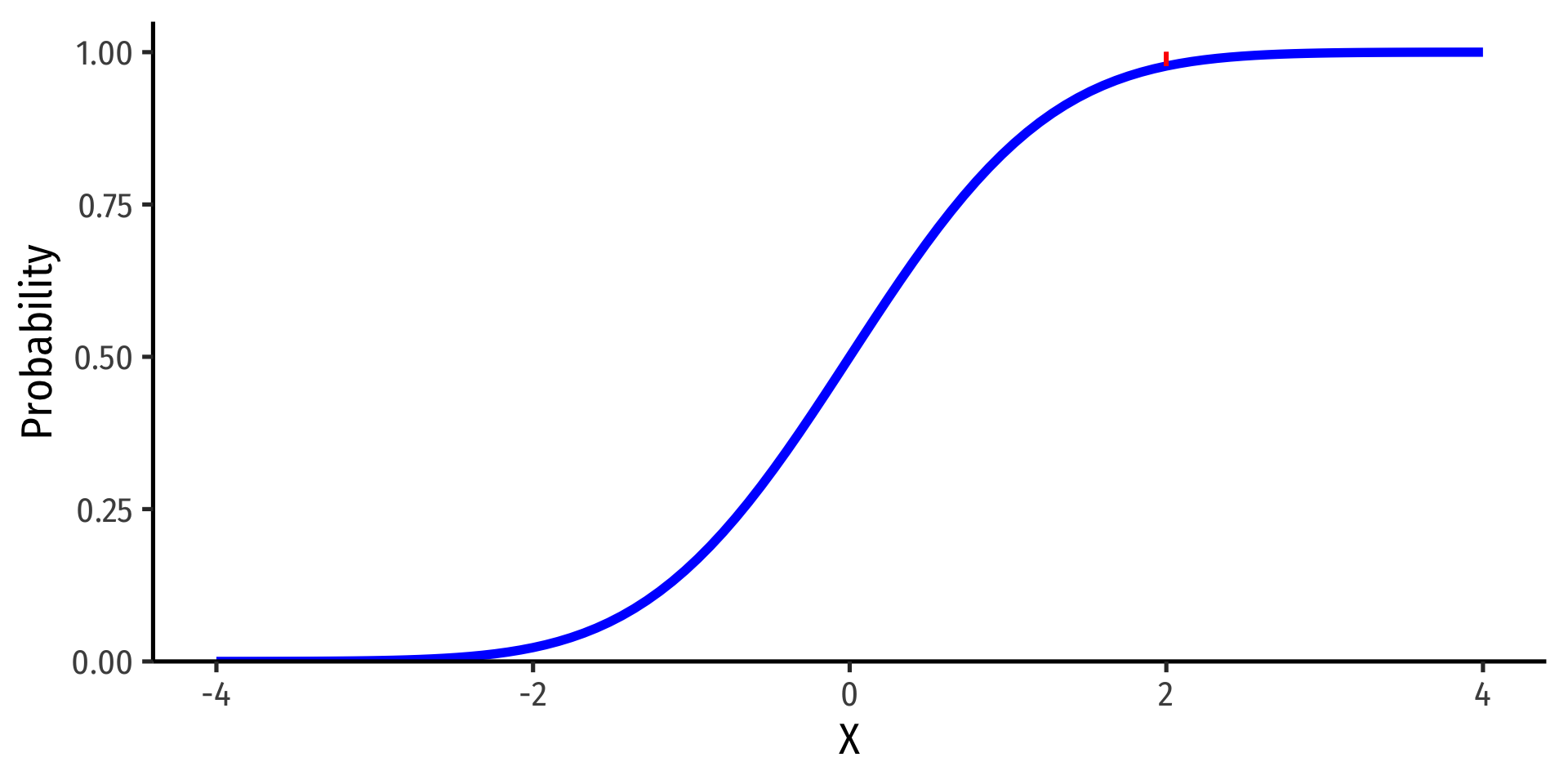
The Standard Normal cdf

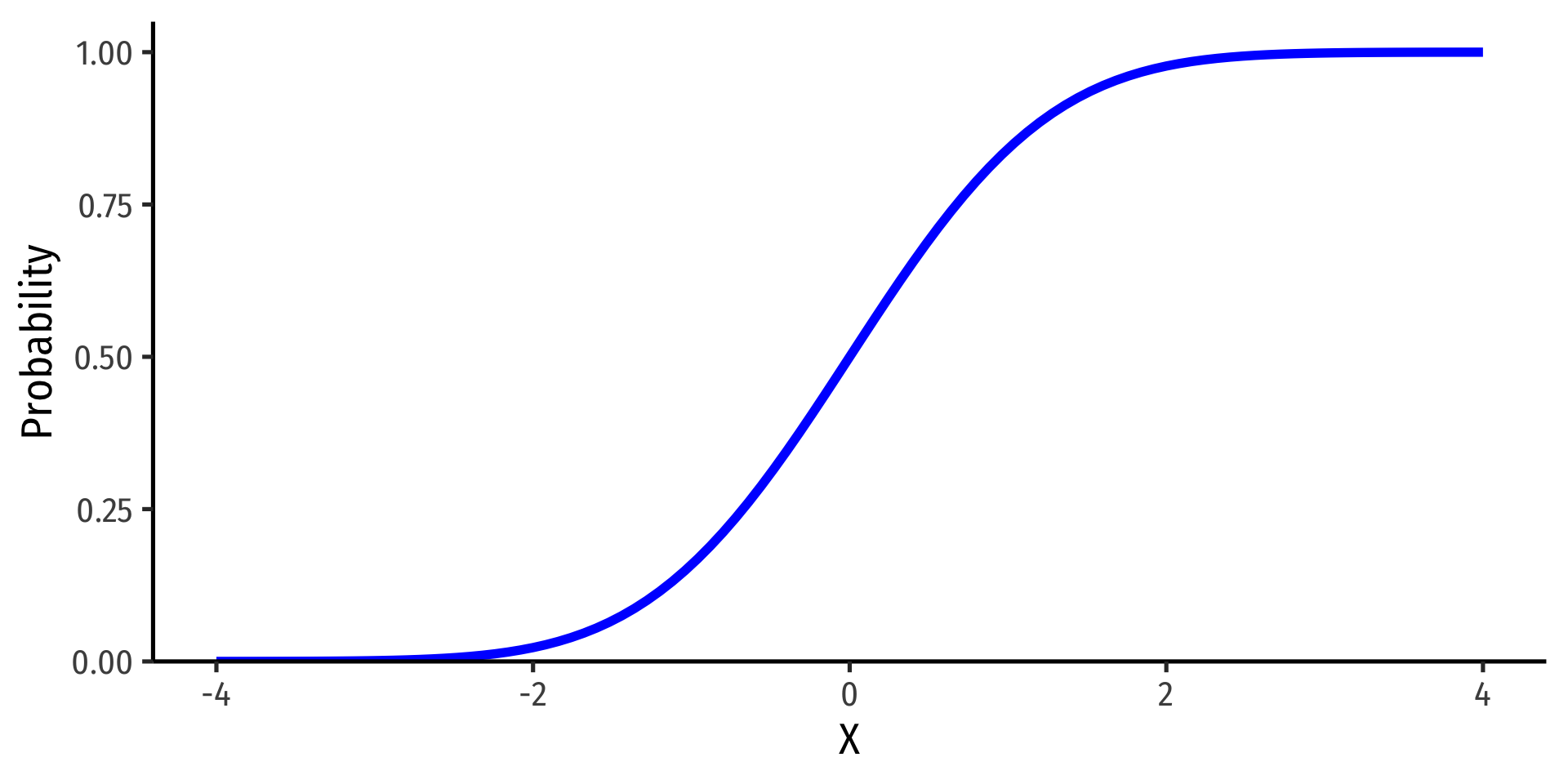
  • The standard normal cdf, often referred to as \(\Phi\):

\[\Phi(k)=P(Z \leq k)\]

(again, the area under the pdf curve to the left of some value \(k\))

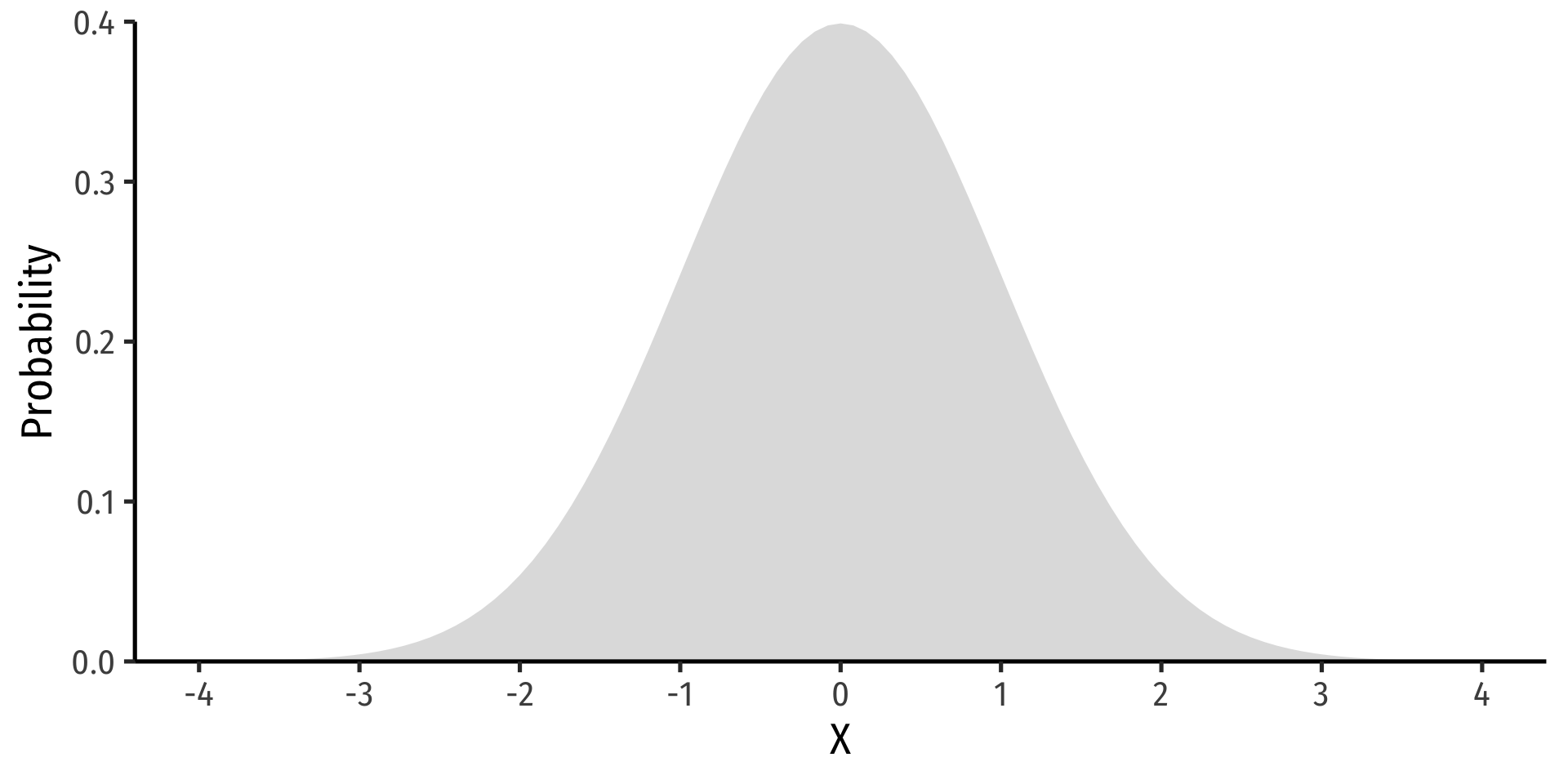
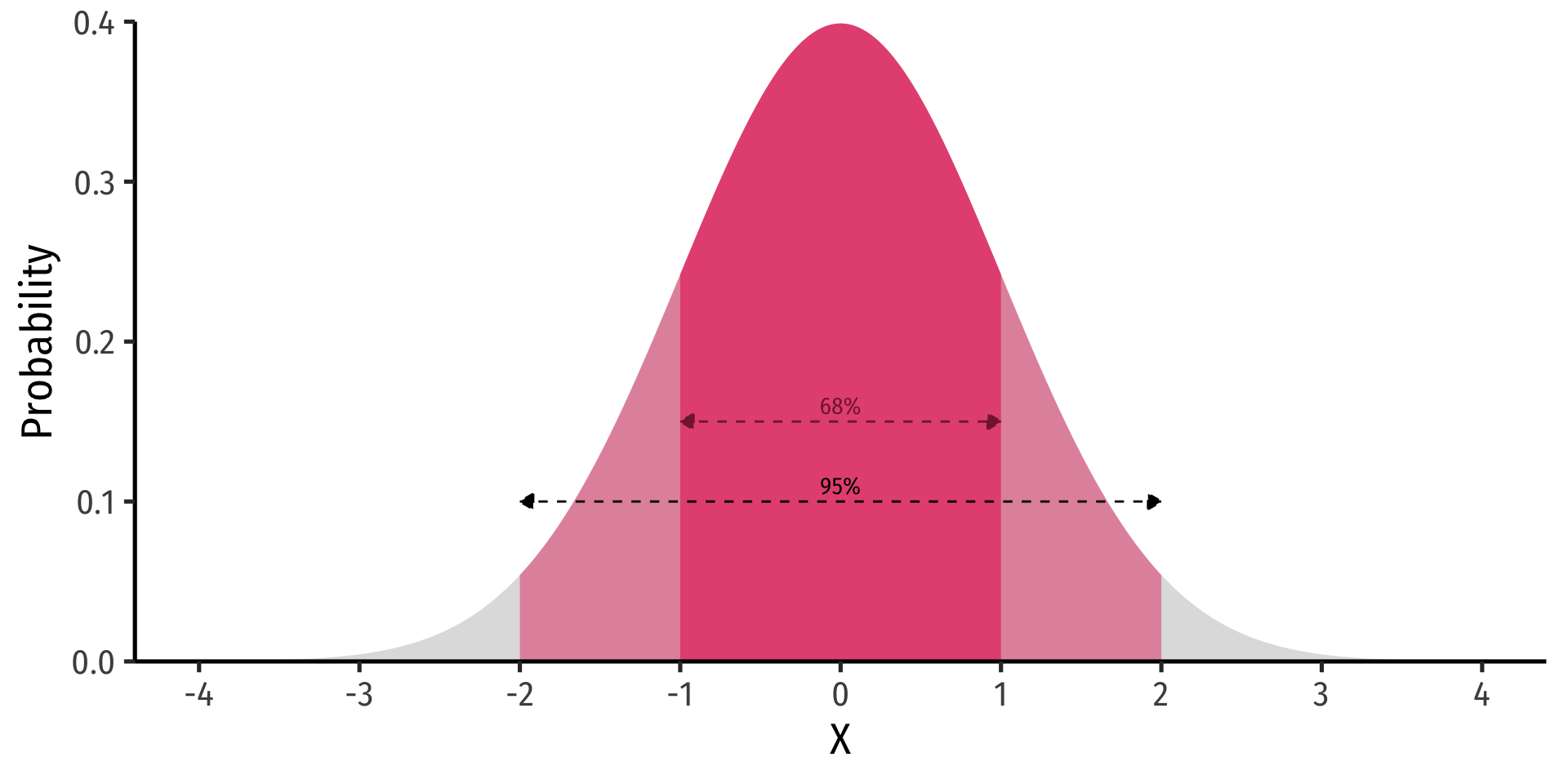
The 68-95-99.7 Empirical Rule

  • 68-95-99.7% empirical rule: for a normal distribution:

The 68-95-99.7 Empirical Rule

  • 68-95-99.7% empirical rule: for a normal distribution:

  • \(P(\mu-1\sigma \leq X \leq \mu+1\sigma) \approx\) 68%

The 68-95-99.7 Empirical Rule

  • 68-95-99.7% empirical rule: for a normal distribution:

  • \(P(\mu-1\sigma \leq X \leq \mu+1\sigma) \approx\) 68%

  • \(P(\mu-2\sigma \leq X \leq \mu+2\sigma) \approx\) 95%

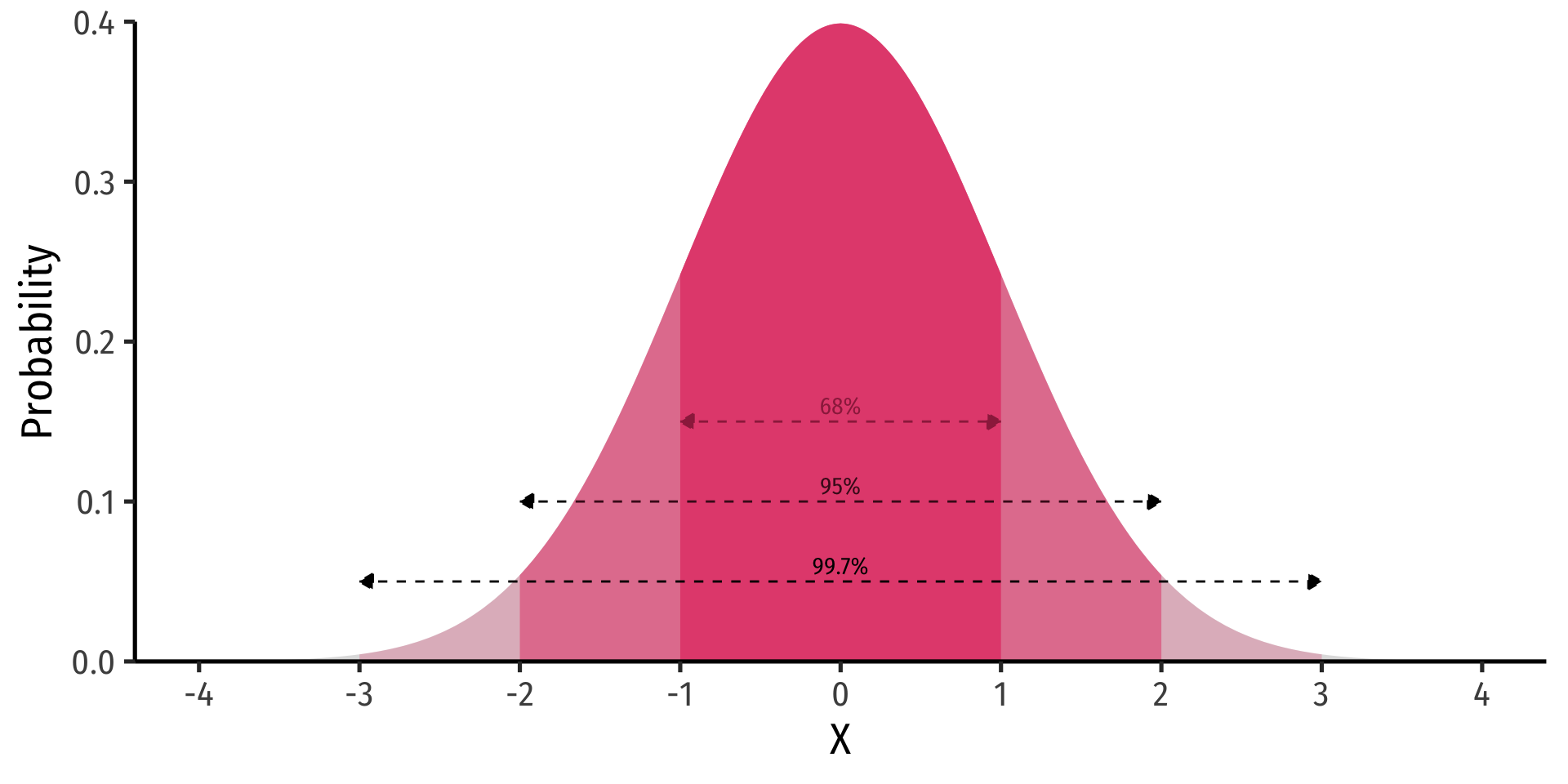
The 68-95-99.7 Empirical Rule

  • 68-95-99.7% empirical rule: for a normal distribution:

  • \(P(\mu-1\sigma \leq X \leq \mu+1\sigma) \approx\) 68%

  • \(P(\mu-2\sigma \leq X \leq \mu+2\sigma) \approx\) 95%

  • \(P(\mu-3\sigma \leq X \leq \mu+3\sigma) \approx\) 99.7%

  • 68/95/99.7% of observations fall within 1/2/3 standard deviations of the mean

Standardizing Normal Distributions

  • We can take any normal distribution (for any \(\mu, \sigma)\) and standardize it to the standard normal distribution by taking the Z-score of any value, \(x_i\):

\[Z=\frac{x_i-\mu}{\sigma}\]

  • Subtract any value by the distribution’s mean and divide by standard deviation

  • \(Z\): number of standard deviations \(x_i\) value is away from the mean

Standardizing Normal Distributions: Example I

Example

On August 8, 2011, the Dow dropped 634.8 points, sending shock waves through the financial community. Assume that during mid-2011 to mid-2012 the daily change for the Dow is normally distributed, with the mean daily change of 1.87 points and a standard deviation of 155.28 points. What is the \(Z\)-score?

\[Z = \frac{X - \mu}{\sigma}\]

\[Z = \frac{634.8-1.87}{155.28}\]

\[Z = -4.1\]

This is 4.1 standard deviations \((\sigma)\) beneath the mean, an extremely low probability event.

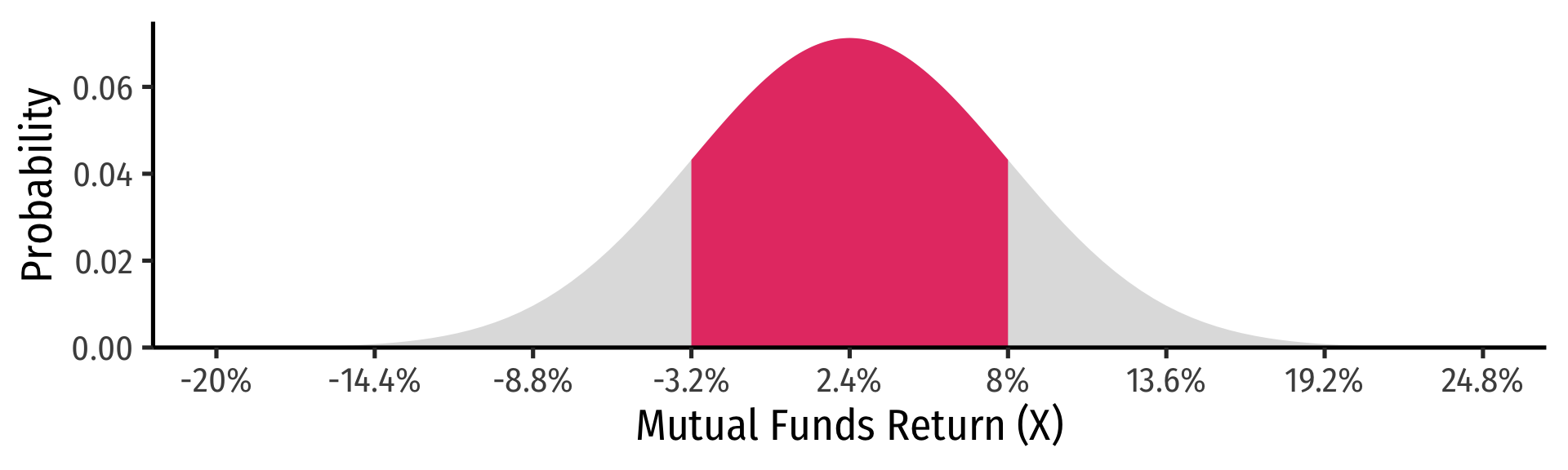
Standardizing Normal Distributions: Example II

Example

In the last quarter of 2021, a group of 64 mutual funds had a mean return of 2.4% with a standard deviation of 5.6%. These returns can be approximated by a normal distribution.

What percent of the funds would you expect to be earning between -3.2% and 8.0% returns?

Convert to standard normal to find \(Z\)-scores for \(8\) and \(-3.2.\)

\[P(-3.2 < X < 8)\]

\[P(\frac{-3.2-2.4}{5.6} < \frac{X-2.4}{5.6} < \frac{8-2.4}{5.6})\]

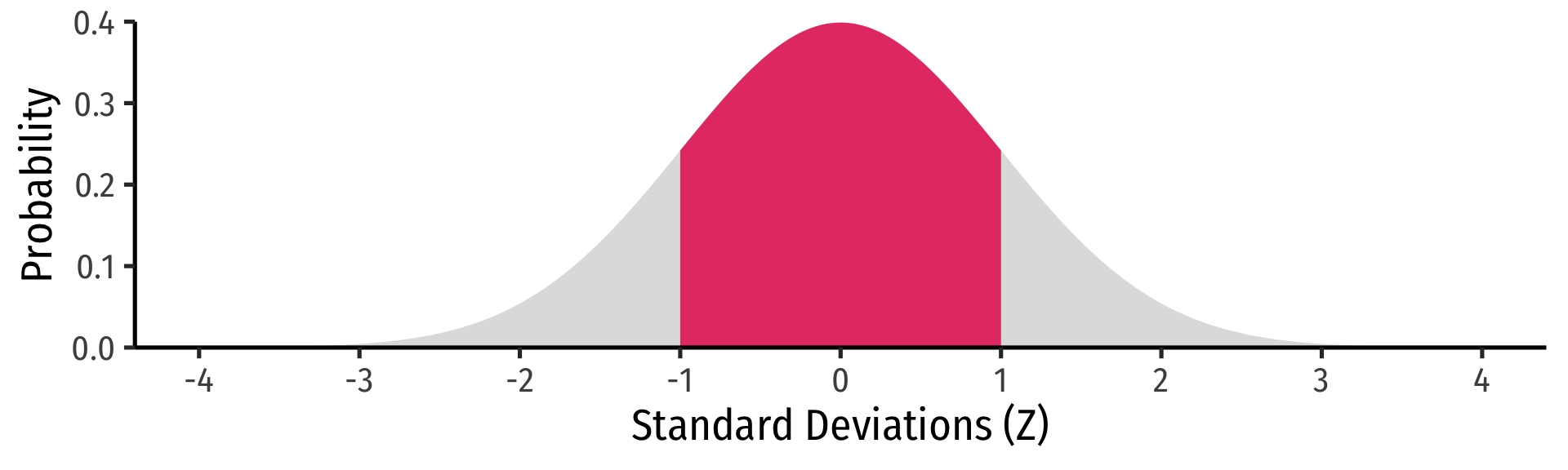
\[P(-1 < Z < 1)\]

\[P(X \pm 1\sigma)=0.68\]

Standardizing Normal Distributions: Example II

Standardizing Normal Distributions: Example III

Example

In the last quarter of 2021, a group of 64 mutual funds had a mean return of 2.4% with a standard deviation of 5.6%. These returns can be approximated by a normal distribution.

  1. What percent of the funds would you expect to be earning 2.4% or less?

  2. What percent of the funds would you expect to be earning between -8.8% and 13.6%?

  3. What percent of the funds would you expect to be earning returns greater than 13.6%?

How do we actually find the probabilities for Z−scores?

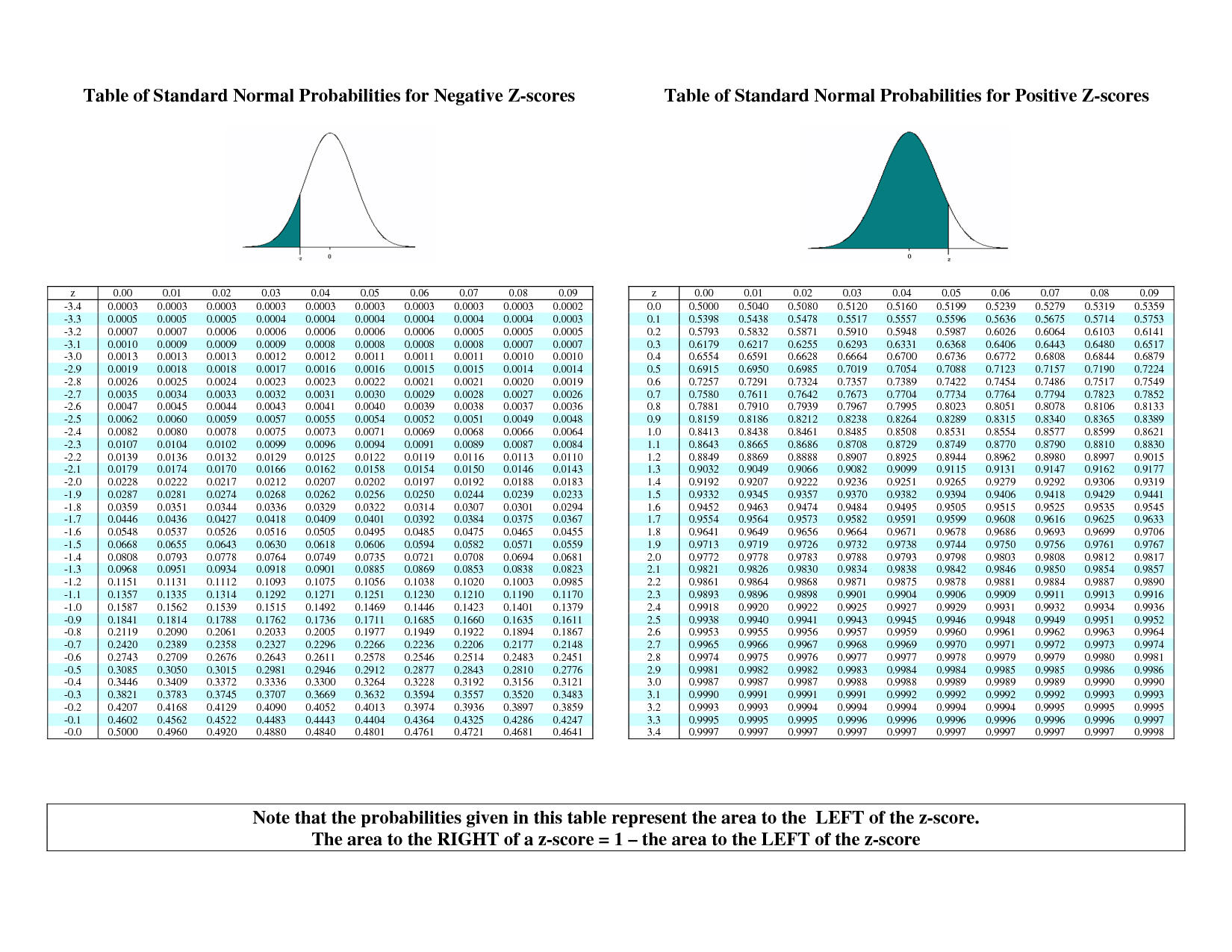
Finding Z-score Probabilities I

Probability to the left of \(z_i\)

\[P(Z \leq z_i)= \underbrace{\Phi(z_i)}_{\text{cdf of }z_i}\]

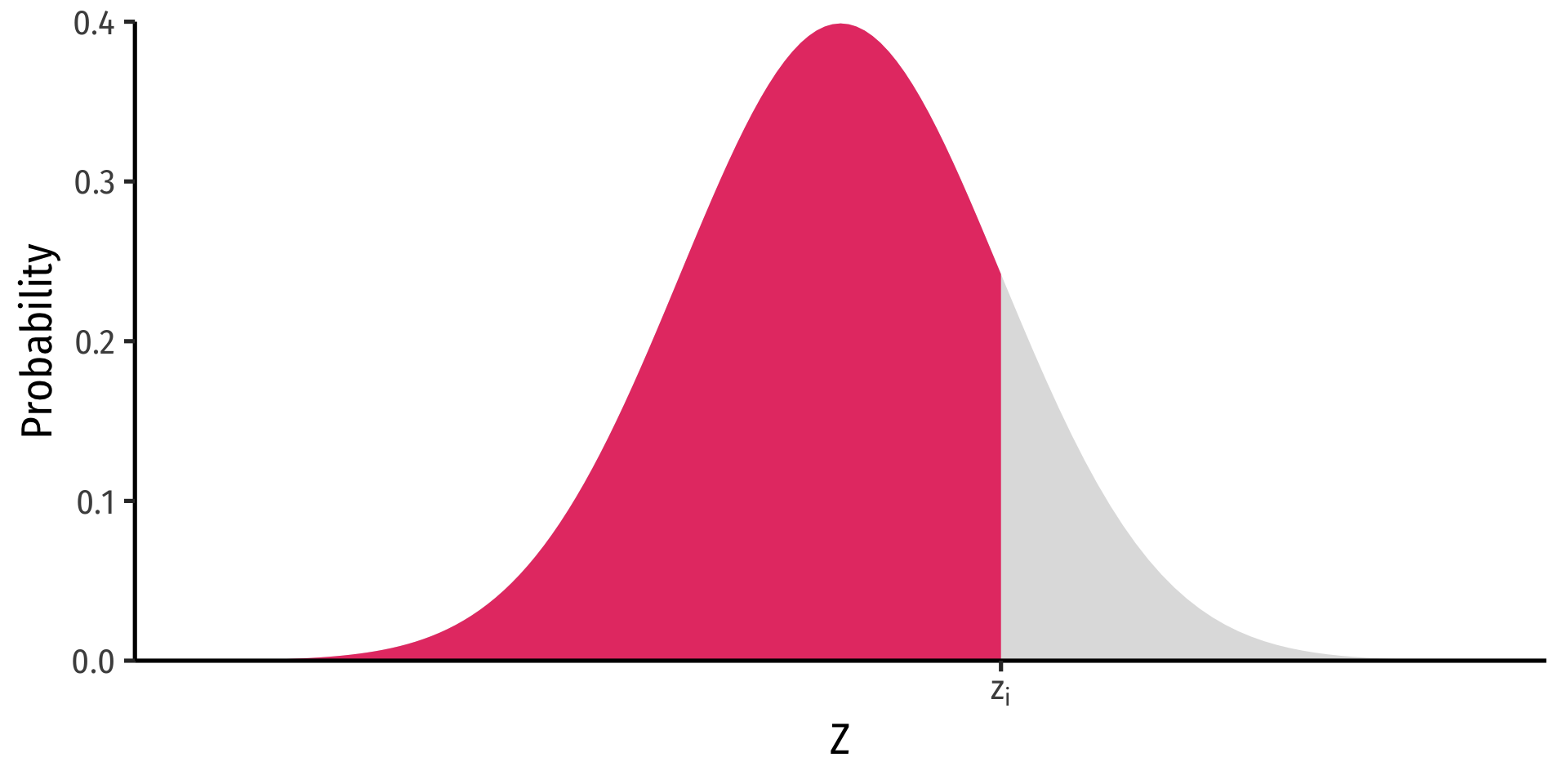
Probability to the right of \(z_i\)

\[P(Z \geq z_i)= 1-\underbrace{\Phi(z_i)}_{\text{cdf of }z_i}\]

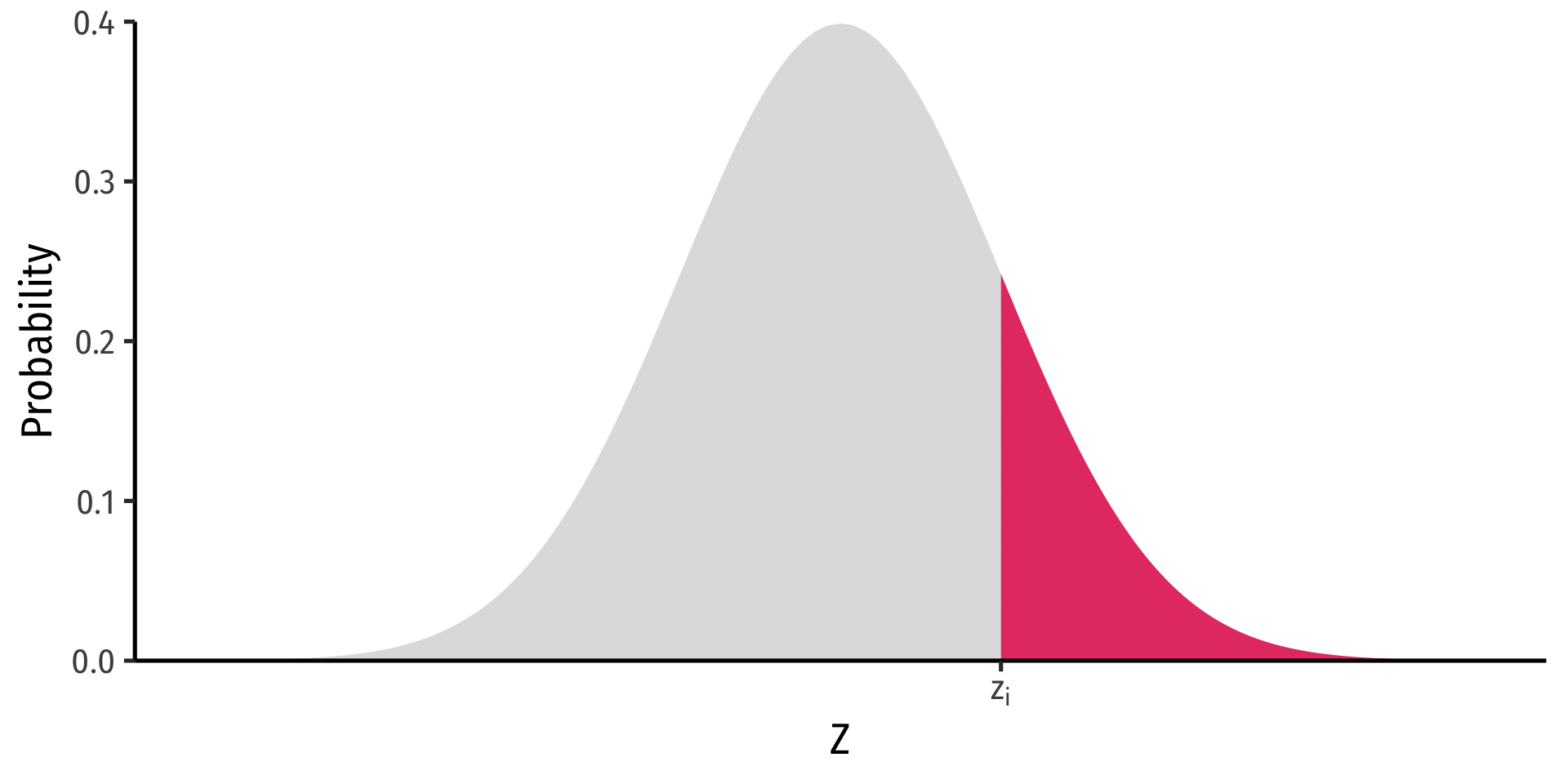
Finding Z-score Probabilities II

Probability between \(z_1\) and \(z_2\)

\[P(z_1 \geq Z \geq z_2)= \underbrace{\Phi(z_2)}_{\text{cdf of }z_2} - \underbrace{\Phi(z_1)}_{\text{cdf of }z_1}\]

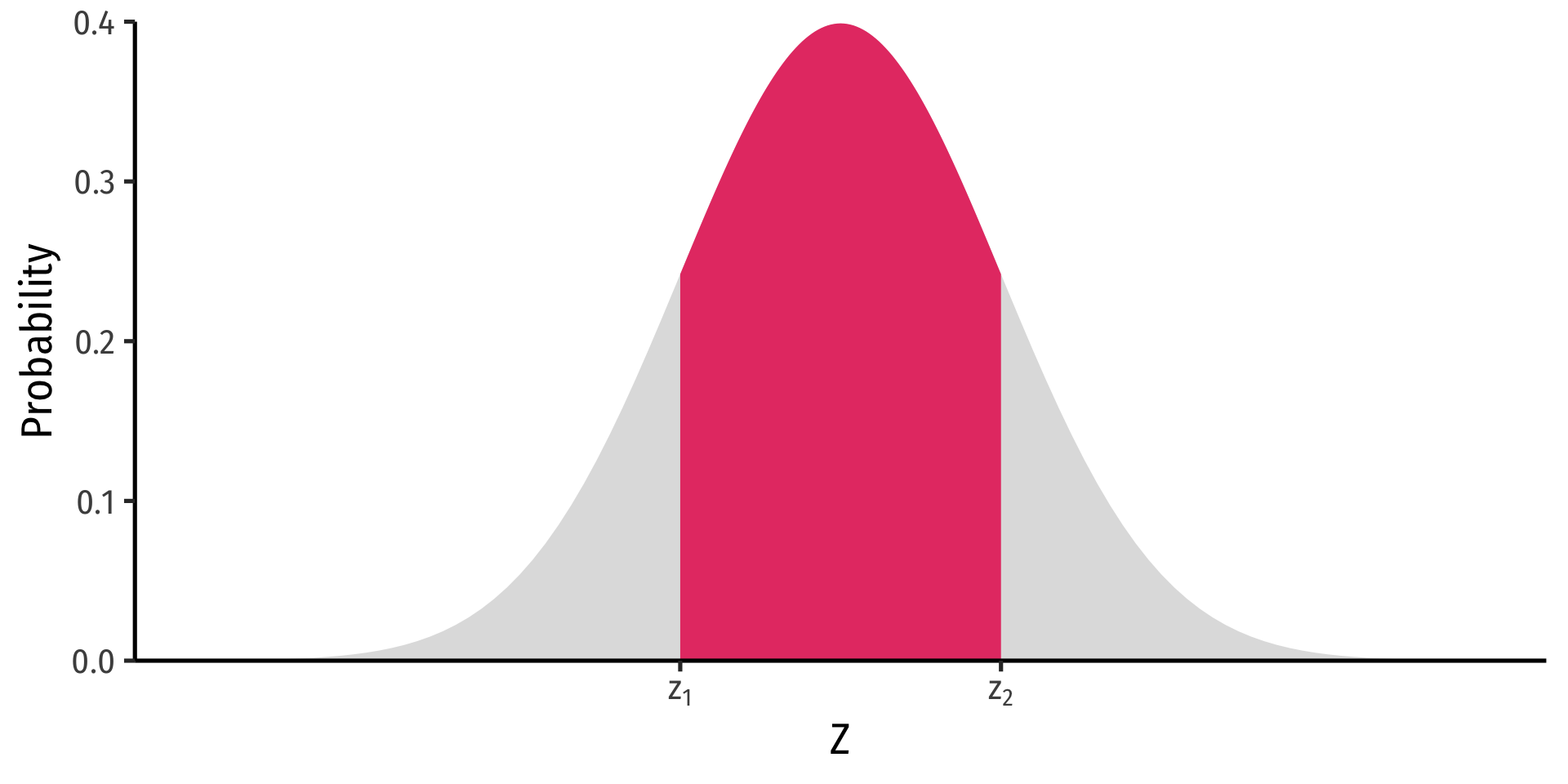
Finding Z-score Probabilities III

  • pnorm() calculates probabilities with a normal distribution with arguments:
    • x = the value
    • mean = the mean
    • sd = the standard deviation
    • lower.tail =
      • TRUE if looking at area to LEFT of value
      • FALSE if looking at area to RIGHT of value

Finding Z-score Probabilities IV

Example

Let the distribution of grades be normal, with mean 75 and standard deviation 10.

  • Probability a student gets at least an 80
pnorm(80, 
      mean = 75,
      sd = 10,
      lower.tail = FALSE) # looking to right
[1] 0.3085375

Finding Z-score Probabilities V

Example

Let the distribution of grades be normal, with mean 75 and standard deviation 10.

  • Probability a student gets at most an 80
pnorm(80, 
      mean = 75,
      sd = 10,
      lower.tail = TRUE) # looking to left
[1] 0.6914625

Finding Z-score Probabilities VI

Example

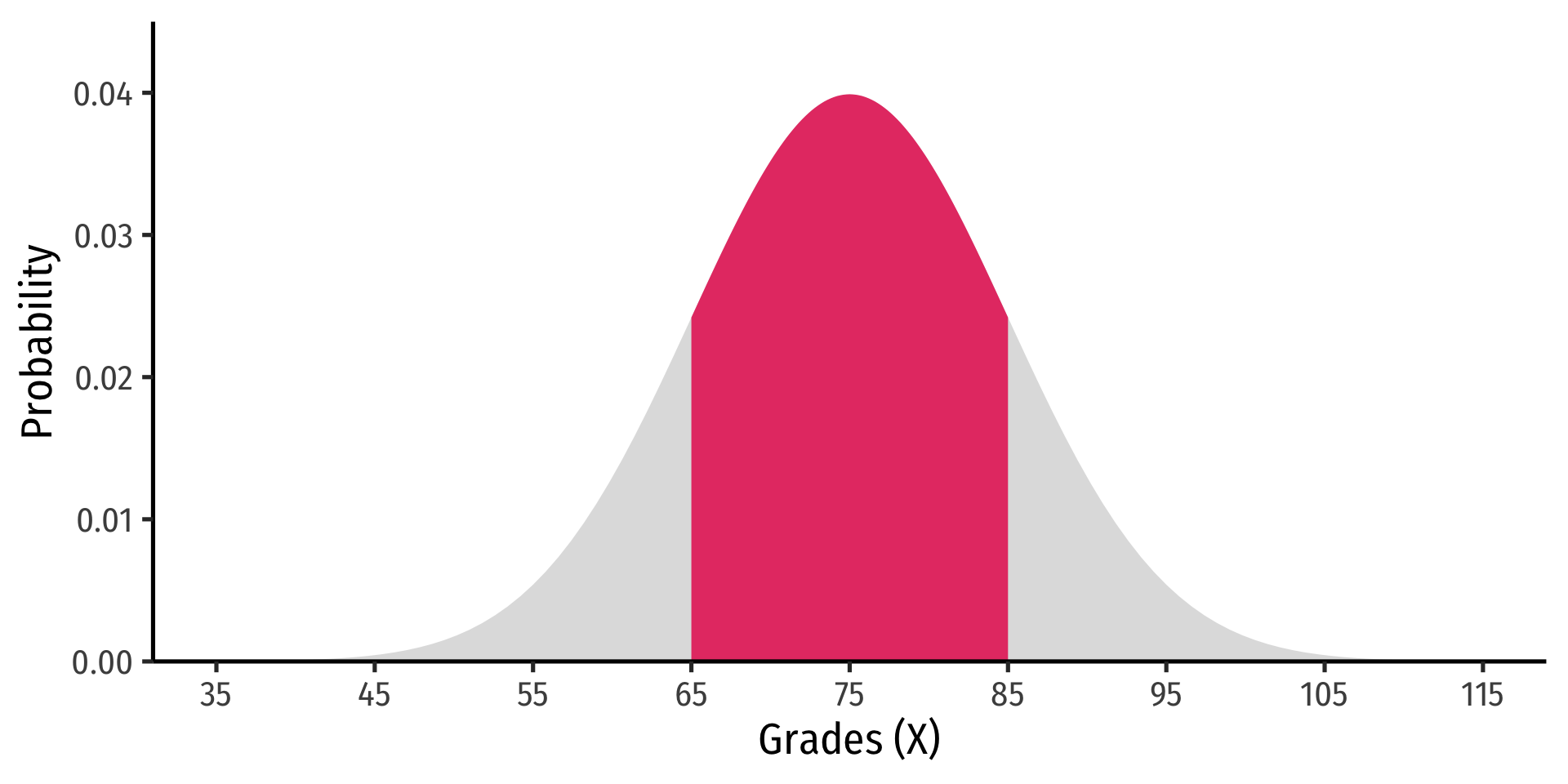
Let the distribution of grades be normal, with mean 75 and standard deviation 10.

  • Probability a student gets between 65 and 85
# subtract two left tails!
pnorm(85, # larger number first!
      mean = 75,
      sd = 10,
      lower.tail = TRUE) - # looking to left, & SUBTRACT
  pnorm(65, # smaller number second!
        mean = 75,
        sd = 10,
        lower.tail = TRUE) #looking to left
[1] 0.6826895

ECON 480 — Econometrics