2.3 — Simple Linear Regression

ECON 480 • Econometrics • Fall 2022

Dr. Ryan Safner
Associate Professor of Economics

safner@hood.edu
ryansafner/metricsF22
metricsF22.classes.ryansafner.com

Contents

Exploring Relationships

Quantifying Relationships

Linear Regression

Deriving OLS Estimators

Our Class Size Example in R

Exploring Relationships

Bivariate Data and Relationships I

  • We looked at single variables for descriptive statistics
  • Most uses of statistics in economics and business investigate relationships between variables

Examples

  • # of police & crime rates
  • healthcare spending & life expectancy
  • government spending & GDP growth
  • carbon dioxide emissions & temperatures

Bivariate Data and Relationships II

  • We will begin with bivariate data for relationships between X and Y

  • Immediate aim is to explore associations between variables, quantified with correlation and linear regression

  • Later we want to develop more sophisticated tools to argue for causation

Bivariate Data: Spreadsheets I

ABCDEFGHIJ0123456789
...1
<dbl>
Country
<chr>
ISO
<chr>
ef
<dbl>
gdp
<dbl>
1AlbaniaALB7.404543.0880
2AlgeriaDZA5.154784.1943
3AngolaAGO5.084153.1463
4ArgentinaARG4.8110501.6603
5AustraliaAUS7.9354688.4459
6AustriaAUT7.5647603.7968
7BahrainBHR7.6022347.9708
8BangladeshBGD6.35972.8807
9BelgiumBEL7.5145181.4382
10BeninBEN6.22804.7240
Next
123456
...
12
Previous
1-10 of 112 rows | 1-5 of 6 columns
  • Rows are individual observations (countries)
  • Columns are variables on all individuals

Bivariate Data: Spreadsheets II

econfreedom %>%
  glimpse()
Rows: 112
Columns: 6
$ ...1      <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 1…
$ Country   <chr> "Albania", "Algeria", "Angola", "Argentina", "Australia", "A…
$ ISO       <chr> "ALB", "DZA", "AGO", "ARG", "AUS", "AUT", "BHR", "BGD", "BEL…
$ ef        <dbl> 7.40, 5.15, 5.08, 4.81, 7.93, 7.56, 7.60, 6.35, 7.51, 6.22, …
$ gdp       <dbl> 4543.0880, 4784.1943, 4153.1463, 10501.6603, 54688.4459, 476…
$ continent <chr> "Europe", "Africa", "Africa", "Americas", "Oceania", "Europe…

Bivariate Data: Spreadsheets III

source("summaries.R")
econfreedom %>%
  summary_table(ef, gdp)
ABCDEFGHIJ0123456789
Variable
<chr>
Obs
<dbl>
Min
<dbl>
Q1
<dbl>
Median
<dbl>
ef1124.816.427.0
gdp112206.711307.465123.3
2 rows | 1-5 of 9 columns

Bivariate Data: Scatterplots I

  • Plot
  • Code

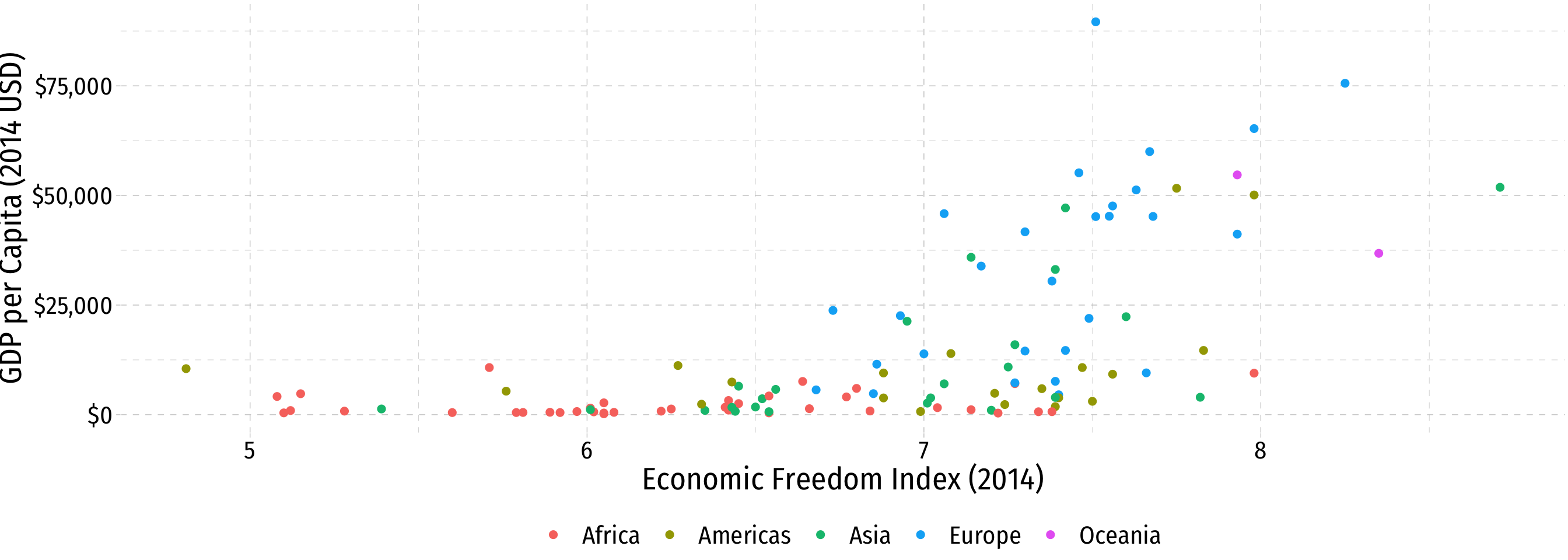
ggplot(data = econfreedom)+
  aes(x = ef,
      y = gdp)+
  geom_point(aes(color = continent),
             size = 2)+
  labs(x = "Economic Freedom Index (2014)",
       y = "GDP per Capita (2014 USD)",
       color = "")+
  scale_y_continuous(labels = scales::dollar)+
  theme_pander(base_family = "Fira Sans Condensed",
           base_size=20)+
  theme(legend.position = "bottom")

Bivariate Data: Scatterplots II

  • Look for association between independent and dependent variables

  1. Direction: is the trend positive or negative?

  2. Form: is the trend linear, quadratic, something else, or no pattern?

  3. Strength: is the association strong or weak?

  4. Outliers: do any observations deviate from the trends above?

Quantifying Relationships

Covariance

  • For any two variables, we can measure their sample covariance, cov(X,Y) or sX,Y to quantify how they vary together1

sX,Y=E[(X−ˉX)(Y−ˉY)]

  • Intuition: if xi is above the mean of X, would we expect the associated yi:
    • to be above the mean of Y also (X and Y covary positively)
    • to be below the mean of Y (X and Y covary negatively)
  • Covariance is a common measure, but the units are meaningless, thus we rarely need to use it so don’t worry about learning the formula

  1. Henceforth we limit all measures to samples, for convenience. Population covariance is denoted σX,Y

Covariance, in R

econfreedom %>%
  summarize(covariance = cov(ef, gdp))
# A tibble: 1 × 1
  covariance
       <dbl>
1      8923.

8923 what, exactly?

Correlation

  • Better to standardize covariance into a more intuitive concept: correlation, rX,Y ∈[−1,1]

rX,Y=sX,YsXsY=cov(X,Y)sd(X)sd(Y)

  • Simply weight covariance by the product of the standard deviations of X and Y
  • Alternatively, take the average1 of the product of standardized (Z-scores for) each (xi,yi) pair:2

r=1n−1n∑i=1(xi−ˉXsX)(yi−ˉYsY)r=1n−1n∑i=1ZXZY

  1. Over n-1, a sample statistic!

  2. See today’s appendix page for example code to calculate correlation “by hand” in R using the second method.

Correlation: Interpretation

  • Correlation is standardized to

−1≤r≤1

  • Negative values ⟹ negative association

  • Positive values ⟹ positive association

  • Correlation of 0 ⟹ no association

  • As |r|→1⟹ the stronger the association

  • Correlation of |r|=1⟹ perfectly linear

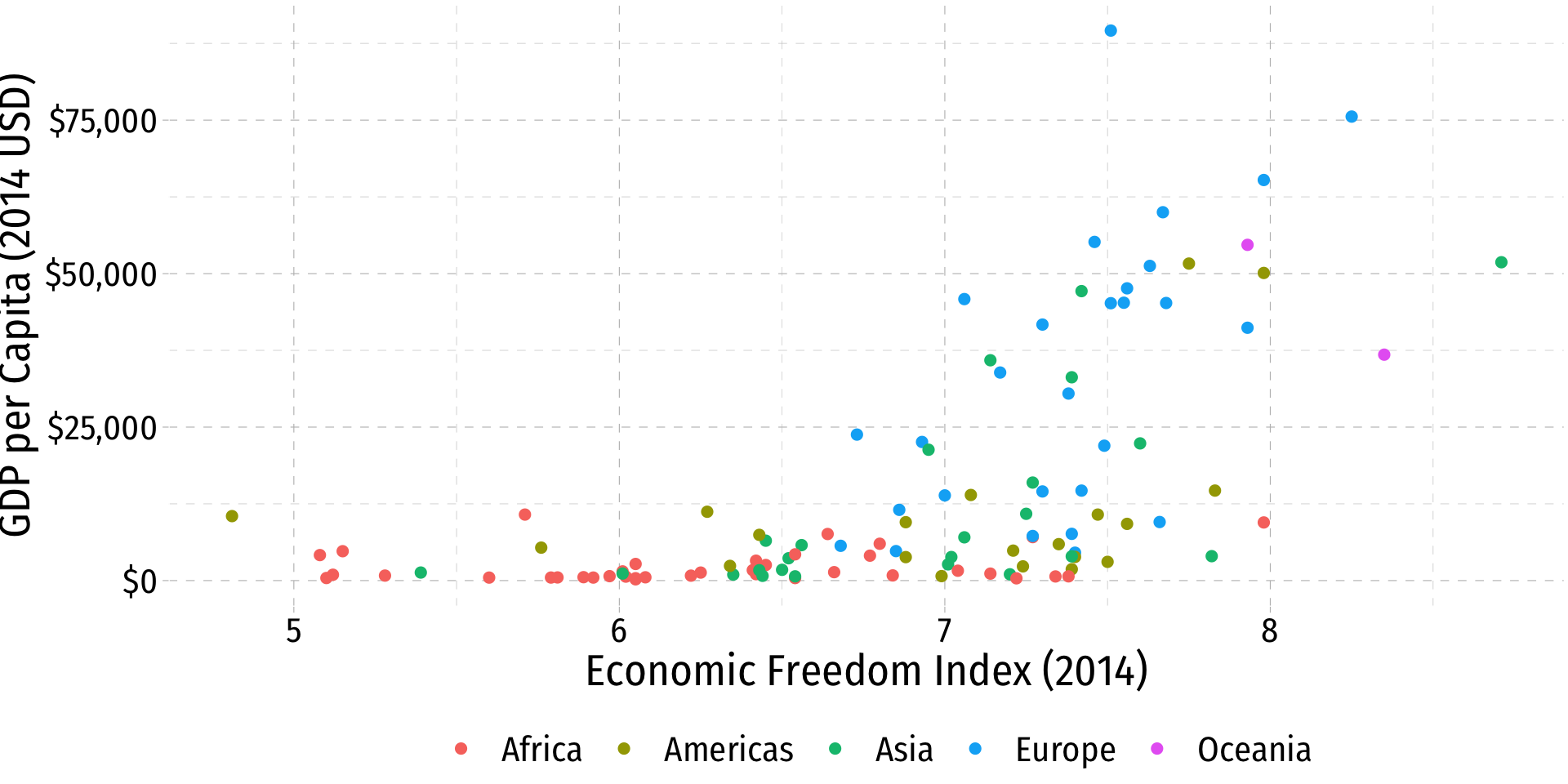
Guess the Correlation!

Guess the Correlation Game

Correlation and Covariance in R

econfreedom %>%
  summarize(covariance = cov(ef, gdp),
            correlation = cor(ef, gdp))
# A tibble: 1 × 2
  covariance correlation
       <dbl>       <dbl>
1      8923.       0.587

Correlation and Endogeneity

  • Your Occasional Reminder: Correlation does not imply causation!

    • I’ll show you the difference in a few weeks (when we can actually talk about causation)

  • If X and Y are strongly correlated, X can still be endogenous!

  • See today’s appendix page for more on Covariance and Correlation

Always Plot Your Data!

Linear Regression

Fitting a Line to Data

  • If an association appears linear, we can estimate the equation of a line that would “fit” the data

Y=a+bX

  • A linear equation describing a line has two parameters:
    • a: vertical intercept
    • b: slope

Fitting a Line to Data

  • If an association appears linear, we can estimate the equation of a line that would “fit” the data

Y=a+bX

  • A linear equation describing a line has two parameters:
    • a: vertical intercept
    • b: slope
  • How do we choose the equation that best fits the data?

Fitting a Line to Data

  • If an association appears linear, we can estimate the equation of a line that would “fit” the data

Y=a+bX

  • A linear equation describing a line has two parameters:

    • a: vertical intercept
    • b: slope

  • How do we choose the equation that best fits the data?

  • This process is called linear regression

Population Linear Regression Model

  • Linear regression lets us estimate the slope of the population regression line between X and Y using sample data

  • We can make statistical inferences about what the true population slope coefficient is

    • eventually & hopefully: a causal inference

  • slope=ΔYΔX: for a 1-unit change in X, how many units will this cause Y to change?

Class Size Example

Example

What is the relationship between class size and educational performance?

Class Size Example: Data Import

# Load the Data

# install.packages("haven") # install for first use

# Packages
library("haven") # load for importing .dta files

# Import and save as ca_school

ca_school <- read_dta("../files/data/caschool.dta")

Data are student-teacher-ratio and average test scores on Stanford 9 Achievement Test for 5th grade students for 420 K-6 and K-8 school districts in California in 1999, (Stock and Watson, 2015: p. 141)

Class Size Example: Data

ca_school %>%
  glimpse()
Rows: 420
Columns: 21
$ observat <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18…
$ dist_cod <dbl> 75119, 61499, 61549, 61457, 61523, 62042, 68536, 63834, 62331…
$ county   <chr> "Alameda", "Butte", "Butte", "Butte", "Butte", "Fresno", "San…
$ district <chr> "Sunol Glen Unified", "Manzanita Elementary", "Thermalito Uni…
$ gr_span  <chr> "KK-08", "KK-08", "KK-08", "KK-08", "KK-08", "KK-08", "KK-08"…
$ enrl_tot <dbl> 195, 240, 1550, 243, 1335, 137, 195, 888, 379, 2247, 446, 987…
$ teachers <dbl> 10.90, 11.15, 82.90, 14.00, 71.50, 6.40, 10.00, 42.50, 19.00,…
$ calw_pct <dbl> 0.5102, 15.4167, 55.0323, 36.4754, 33.1086, 12.3188, 12.9032,…
$ meal_pct <dbl> 2.0408, 47.9167, 76.3226, 77.0492, 78.4270, 86.9565, 94.6237,…
$ computer <dbl> 67, 101, 169, 85, 171, 25, 28, 66, 35, 0, 86, 56, 25, 0, 31, …
$ testscr  <dbl> 690.80, 661.20, 643.60, 647.70, 640.85, 605.55, 606.75, 609.0…
$ comp_stu <dbl> 0.34358975, 0.42083332, 0.10903226, 0.34979424, 0.12808989, 0…
$ expn_stu <dbl> 6384.911, 5099.381, 5501.955, 7101.831, 5235.988, 5580.147, 5…
$ str      <dbl> 17.88991, 21.52466, 18.69723, 17.35714, 18.67133, 21.40625, 1…
$ avginc   <dbl> 22.690001, 9.824000, 8.978000, 8.978000, 9.080333, 10.415000,…
$ el_pct   <dbl> 0.000000, 4.583333, 30.000002, 0.000000, 13.857677, 12.408759…
$ read_scr <dbl> 691.6, 660.5, 636.3, 651.9, 641.8, 605.7, 604.5, 605.5, 608.9…
$ math_scr <dbl> 690.0, 661.9, 650.9, 643.5, 639.9, 605.4, 609.0, 612.5, 616.1…
$ aowijef  <dbl> 35.77982, 43.04933, 37.39445, 34.71429, 37.34266, 42.81250, 3…
$ es_pct   <dbl> 1.000000, 3.583333, 29.000002, 1.000000, 12.857677, 11.408759…
$ es_frac  <dbl> 0.01000000, 0.03583334, 0.29000002, 0.01000000, 0.12857677, 0…

Class Size Example: Data

ABCDEFGHIJ0123456789
observat
<dbl>
dist_cod
<dbl>
county
<chr>
district
<chr>
gr_span
<chr>
175119AlamedaSunol Glen UnifiedKK-08
261499ButteManzanita ElementaryKK-08
361549ButteThermalito Union ElementaryKK-08
461457ButteGolden Feather Union ElementaryKK-08
561523ButtePalermo Union ElementaryKK-08
662042FresnoBurrel Union ElementaryKK-08
768536San JoaquinHolt Union ElementaryKK-08
863834KernVineland ElementaryKK-08
962331FresnoOrange Center ElementaryKK-08
1067306SacramentoDel Paso Heights ElementaryKK-06
Next
123456
...
42
Previous
1-10 of 420 rows | 1-5 of 21 columns

Class Size Example: Scatterplot

  • Plot
  • Code

ggplot(data = ca_school)+
  aes(x = str,
      y = testscr)+
  geom_point(color = "blue")+
  labs(x = "Student to Teacher Ratio",
       y = "Test Score")+
  theme_bw(base_family = "Fira Sans Condensed",
           base_size = 20)

Class Size Example: Slope I

  • If we change (Δ) the class size by an amount, what would we expect the change in test scores to be?

β=change in test scorechange in class size=Δtest scoreΔclass size

  • If we knew β, we could say that changing class size by 1 student will change test scores by β

Class Size Example: Slope II

  • Rearranging:

Δtest score=β×Δclass size

Class Size Example: Slope III

  • Rearranging:

Δtest score=β×Δclass size

  • Suppose β=−0.6. If we shrank class size by 2 students, our model predicts:

Δtest score=−2×βΔtest score=−2×−0.6Δtest score=1.2

Test scores would improve by 1.2 points, on average.

Class Size Example: Slope and Average Effect

test score=β0+β1×class size

  • The line relating class size and test scores has the above equation

  • β0 is the vertical-intercept, test score where class size is 0

  • β1 is the slope of the regression line

  • This relationship only holds on average for all districts in the population, individual districts are also affected by other factors

Class Size Example: Marginal Effect

  • To get an equation that holds for each district, we need to include other factors

test score=β0+β1class size+other factors

  • For now, we will ignore these until Unit III

  • Thus, β0+β1class size gives the average effect of class sizes on scores

  • Later, we will want to estimate the marginal effect (causal effect) of each factor on an individual district’s test score, holding all other factors constant

Econometric Models: Overview I

Y=β0+β1X+u

  • Y is the dependent variable of interest
    • AKA “response variable,” “regressand,” “Left-hand side (LHS) variable”
  • X1 is an independent variable
    • AKA “explanatory variable”, “regressor,” “Right-hand side (RHS) variable”, “covariate”
  • Our data consists of a spreadsheet of observed values of (X1i,X2i,Yi)

Econometric Models: Overview II

Y=β0+β1X+u

  • To model, we “regress Y on X1”
  • β0 and β1 are parameters that describe the population relationships between the variables
    • unknown! to be estimated
  • u is a random error term
    • ’U’nobservable, we can’t measure it, and must model with assumptions about it

The Population Regression Model

  • How do we draw a line through the scatterplot? We do not know the “true” β0 or β1

  • We do have data from a sample of class sizes and test scores

  • So the real question is, how can we estimate β0 and β1?

Deriving OLS Estimators

Actual, Predicted, and Residual Values

  • With a simple linear regression model, for each associated X value, we have
  1. The observed (or actual) values of Yi

Actual, Predicted, and Residual Values

  • With a simple linear regression model, for each associated X value, we have
  1. The observed (or actual) values of Yi
  2. Predicted (or fitted) values, ˆYi

Actual, Predicted, and Residual Values

  • With a simple linear regression model, for each associated X value, we have
  1. The observed (or actual) values of Yi
  2. Predicted (or fitted) values, ˆYi
  3. The residual (or error), ˆui=Yi−ˆYi … the difference between predicted and observed values

Yi=ˆYi+ˆuiObservedi=Modeli+Errori

Deriving OLS Estimators

  • Take the residuals ˆui and square them (why)?

Deriving OLS Estimators

  • Take the residuals ˆui and square them (why)?

  • The regression line minimizes the sum of the squared residuals (SSR)

SSR=n∑i=1ˆui2

O-rdinary L-east S-quares Estimators

  • The Ordinary Least Squares (OLS) estimators of the unknown population parameters β0 and β1, solve the calculus problem:

minβ0,β1n∑i=1[Yi−(β0+β1Xi⏟^Yi)⏟^ui]2

  • Intuitively, OLS estimators minimize the sum of the squared residuals (distance between the actual values Yi and the predicted values ^Yi) along the estimated regression line

The OLS Regression Line

  • The OLS regression line or sample regression line is the linear function constructed using the OLS estimators:

^Yi=^β0+^β1Xi

  • ^β0 and ^β1 (“beta 0 hat” & “beta 1 hat”) are the OLS estimators of population parameters β0 and β1 using sample data
  • The predicted value of Y given X, based on the regression, is E(Yi|Xi)=^Yi
  • The residual or prediction error for the ith observation is the difference between observed Yi and its predicted value, ^ui=Yi−^Yi

The OLS Regression Estimators

  • The solution to the SSE minimization problem yields:1

ˆβ0=ˉY−ˆβ1ˉX

ˆβ1=n∑i=1(Xi−ˉX)(Yi−ˉY)n∑i=1(Xi−ˉX)2=sXYs2X=cov(X,Y)var(X)

  1. See next class’ appendix page for proofs.

(Some) Properties of OLS

  1. The regression line goes through the “center of mass” point (ˉX,ˉY)
  • Again, ˆβ0=ˉY−ˆβ1ˉX
  1. The slope, ˆβ1 has the same sign as the correlation coefficient rX,Y, and is related

ˆβ1=rsYsX

  1. The residuals sum and average to zero

n∑i=1ˆui=0E[ˆu]=0

  1. The residuals and X are uncorrelated

Our Class Size Example in R

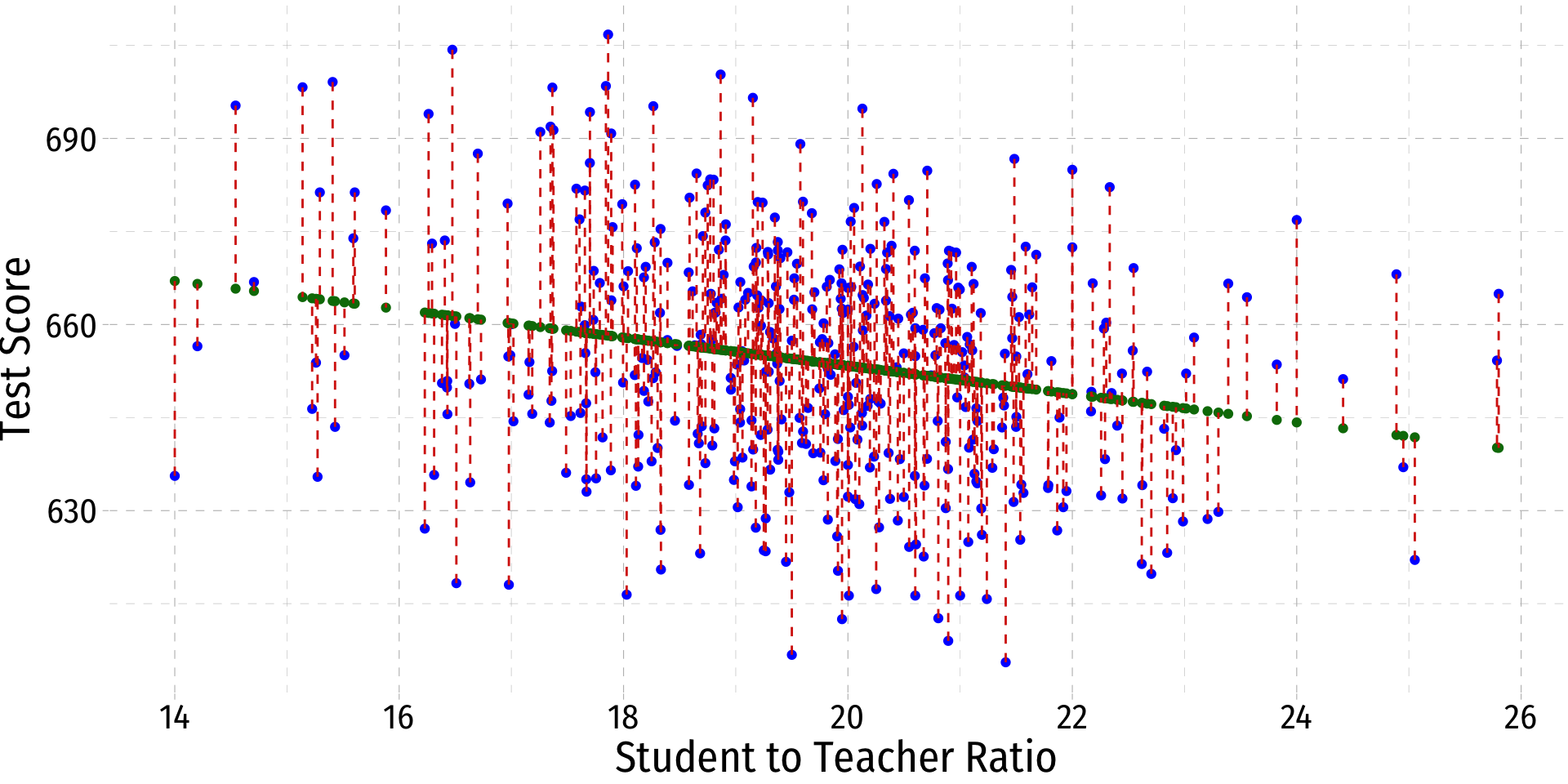
Class Size Scatterplot (Again)

  • There is some true (unknown) population relationship:

test scorei=β0+β1stri

  • β1=Δtest scoreΔstr=??

Class Size Scatterplot with Regression Line

Code 
scatter+
  geom_smooth(method = "lm", color = "red")

Linear Regression in R I

# run regression of testscr on str
school_reg <- lm(testscr ~ str, 
                 data = ca_school)

Format for regression is lm(y ~ x, data = df)

  • y is dependent variable (listed first!)

  • ~ means “is modeled by” or “is explained by”

  • x is the independent variable

  • df is name of dataframe where data is stored

This is base R (there’s no good tidyverse way to do this yet…ish1)

  1. tidymodels appears to be the new contender. It is used primarily for machine learning, but standardizes modeling, including OLS, in a tidy way. I think it’s a bit unnecessary for us to use, for now.

Linear Regression in R II

# look at reg object
school_reg 

Call:
lm(formula = testscr ~ str, data = ca_school)

Coefficients:
(Intercept)          str  
     698.93        -2.28
  • Stored as an lm object called school_reg, a type of list object

Linear Regression in R II

# get full summary
school_reg %>% summary()

Call:
lm(formula = testscr ~ str, data = ca_school)

Residuals:
    Min      1Q  Median      3Q     Max 
-47.727 -14.251   0.483  12.822  48.540 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 698.9330     9.4675  73.825  < 2e-16 ***
str          -2.2798     0.4798  -4.751 2.78e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 18.58 on 418 degrees of freedom
Multiple R-squared:  0.05124,   Adjusted R-squared:  0.04897 
F-statistic: 22.58 on 1 and 418 DF,  p-value: 2.783e-06

  • Looking at the summary, there’s a lot of information here!

  • These objects are cumbersome, come from a much older, pre-tidyverse era of base R

  • Luckily, we now have some more tidy ways of working with regression output!

Tidy Regression with broom

broom.tidyverse.org

  • The broom package allows us to work with regression objects as tidier tibbles

  • Several useful commands:

Command Does
tidy() Create tibble of regression coefficients & stats
glance() Create tibble of regression fit statistics
augment() Create tibble of data with regression-based variables

Tidy Regression with broom: tidy()

  • The tidy() function creates a tidy tibble of regression output
# load packages
library(broom)

# tidy regression output
school_reg %>% 
  tidy()
# A tibble: 2 × 5
  term        estimate std.error statistic   p.value
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)   699.       9.47      73.8  6.57e-242
2 str            -2.28     0.480     -4.75 2.78e-  6

Tidy Regression with broom: tidy()

  • The tidy() function creates a tidy tibble of regression output…with confidence intervals
# load packages
library(broom)

# tidy regression output
school_reg %>%
  tidy(conf.int = TRUE)
# A tibble: 2 × 7
  term        estimate std.error statistic   p.value conf.low conf.high
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>    <dbl>     <dbl>
1 (Intercept)   699.       9.47      73.8  6.57e-242   680.      718.  
2 str            -2.28     0.480     -4.75 2.78e-  6    -3.22     -1.34

Tidy Regression with broom: glance()

  • glance() shows us a lot of overall regression statistics and diagnostics
    • We’ll interpret these in next class and beyond
# look at regression statistics and diagnostics
school_reg %>% 
  glance()
# A tibble: 1 × 12
  r.squ…¹ adj.r…² sigma stati…³ p.value    df logLik   AIC   BIC devia…⁴ df.re…⁵
    <dbl>   <dbl> <dbl>   <dbl>   <dbl> <dbl>  <dbl> <dbl> <dbl>   <dbl>   <int>
1  0.0512  0.0490  18.6    22.6 2.78e-6     1 -1822. 3650. 3663. 144315.     418
# … with 1 more variable: nobs <int>, and abbreviated variable names
#   ¹​r.squared, ²​adj.r.squared, ³​statistic, ⁴​deviance, ⁵​df.residual

Tidy Regression with broom: augment()

  • augment() creates a new tibble with the data (X,Y) and regression-based variables, including:
    • .fitted are fitted (predicted) values from model, i.e. ˆYi
    • .resid are residuals (errors) from model, i.e. ˆui
# add regression-based values to data
school_reg %>% 
  augment()
# A tibble: 420 × 8
   testscr   str .fitted .resid    .hat .sigma  .cooksd .std.resid
     <dbl> <dbl>   <dbl>  <dbl>   <dbl>  <dbl>    <dbl>      <dbl>
 1    691.  17.9    658.   32.7 0.00442   18.5 0.00689       1.76 
 2    661.  21.5    650.   11.3 0.00475   18.6 0.000893      0.612
 3    644.  18.7    656.  -12.7 0.00297   18.6 0.000700     -0.685
 4    648.  17.4    659.  -11.7 0.00586   18.6 0.00117      -0.629
 5    641.  18.7    656.  -15.5 0.00301   18.6 0.00105      -0.836
 6    606.  21.4    650.  -44.6 0.00446   18.5 0.0130       -2.40 
 7    607.  19.5    654.  -47.7 0.00239   18.5 0.00794      -2.57 
 8    609   20.9    651.  -42.3 0.00343   18.5 0.00895      -2.28 
 9    612.  19.9    653.  -41.0 0.00244   18.5 0.00597      -2.21 
10    613.  20.8    652.  -38.9 0.00329   18.5 0.00723      -2.09 
# … with 410 more rows

Class Size Regression Result

  • Using OLS, we find:

^test scorei=689.93−2.28stri

  • ^β0=689.93: test score for str=0
  • ^β1=−2.28: for every 1 unit change in str, ^test_score changes by -2.28 points

test scorei=689.93−2.28stri+ˆui

Class Size Regression Residuals

.resid = testscr - .fitted

ˆui=test scorei−^test scorei

ˆui=test scorei−(689.93−2.28stri)

Class Size Regression: Fitted and Residual Values

aug_reg <- school_reg %>% 
  augment()

aug_reg %>% 
  dplyr::select(testscr, str, .fitted, .resid)
# A tibble: 420 × 4
   testscr   str .fitted .resid
     <dbl> <dbl>   <dbl>  <dbl>
 1    691.  17.9    658.   32.7
 2    661.  21.5    650.   11.3
 3    644.  18.7    656.  -12.7
 4    648.  17.4    659.  -11.7
 5    641.  18.7    656.  -15.5
 6    606.  21.4    650.  -44.6
 7    607.  19.5    654.  -47.7
 8    609   20.9    651.  -42.3
 9    612.  19.9    653.  -41.0
10    613.  20.8    652.  -38.9
# … with 410 more rows

testscr = .fitted + .resid

Class Size Regression: An Example Data Point I

  • One district in our sample is Richmond Elementary
ABCDEFGHIJ0123456789
observat
<dbl>
district
<chr>
testscr
<dbl>
str
<dbl>
dist_cod
<dbl>
355Richmond Elementary672.452264170
1 row | 1-5 of 21 columns
aug_reg %>%
  slice(355) #
ABCDEFGHIJ0123456789
testscr
<dbl>
str
<dbl>
.fitted
<dbl>
.resid
<dbl>
.hat
<dbl>
672.4522648.777223.672840.006093719
1 row | 1-5 of 8 columns

Class Size Regression: An Example Data Point II

  • .fitted value:

^Test ScoreRichmond=698−2.28(22)≈648

  • .resid value:

ˆuRichmond=672−648≈24

Class Size Regression: An Example Data Point III

  • Plot
  • Code

Making Predictions

  • We can use the regression model to make a prediction for a particular xi

Example

Suppose we have a school district with a student/teacher ratio of 18. What is the predicted average district test score?

^test scorei=^β0+^β1stri=698.93−2.28(18)=657.89

Making Predictions In R

  • We can do this in R with the predict()1 function, which requires (at least) two inputs:
    1. An lm object (saved regression)
    2. newdata with X value(s) to predict ˆY for, as a data.frame (or tibble)
some_district <- tibble(str = 18) # make a dataframe of "new data"'

some_district # look at it just to see
# A tibble: 1 × 1
    str
  <dbl>
1    18


predict(school_reg, # regression lm object
        newdata = some_district) # a dataframe of new data)
       1 
657.8964

  1. See more options here

Making Predictions In R, Manually I

  • Of course we could do it ourselves…
# save tidied regression

tidy_reg <- tidy(school_reg)


# look at it, again
tidy_reg
# A tibble: 2 × 5
  term        estimate std.error statistic   p.value
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)   699.       9.47      73.8  6.57e-242
2 str            -2.28     0.480     -4.75 2.78e-  6

Making Predictions In R, Manually II

  • Of course we could do it ourselves…
# extract and save beta_0
beta_0 <- tidy_reg %>%
  filter(term == "(Intercept)") %>%
  pull(estimate)


# check it 
beta_0
[1] 698.933

Making Predictions In R, Manually II

  • Of course we could do it ourselves…
# extract and save beta_1
beta_1 <- tidy_reg %>%
  filter(term == "str") %>%
  pull(estimate)
# check it
beta_1
[1] -2.279808


# predict for str = 18
beta_0 + beta_1 * 18
[1] 657.8964

ECON 480 — Econometrics

1
2.3 — Simple Linear Regression ECON 480 • Econometrics • Fall 2022 Dr. Ryan Safner Associate Professor of Economics safner@hood.edu ryansafner/metricsF22 metricsF22.classes.ryansafner.com

  1. Slides

  2. Tools

  3. Close
  • Title Slide
  • Contents
  • Exploring Relationships
  • Bivariate Data and Relationships I
  • Bivariate Data and Relationships II
  • Bivariate Data: Spreadsheets I
  • Bivariate Data: Spreadsheets II
  • Bivariate Data: Spreadsheets III
  • Bivariate Data: Scatterplots I
  • Bivariate Data: Scatterplots II
  • Quantifying Relationships
  • Covariance
  • Covariance, in R
  • Correlation
  • Correlation: Interpretation
  • Guess the Correlation!
  • Correlation and Covariance in R
  • Correlation and Endogeneity
  • Always Plot Your Data!
  • Linear Regression
  • Fitting a Line to Data
  • Fitting a Line to Data
  • Fitting a Line to Data
  • Population Linear Regression Model
  • Class Size Example
  • Class Size Example: Data Import
  • Class Size Example: Data
  • Class Size Example: Data
  • Class Size Example: Scatterplot
  • Class Size Example: Slope I
  • Class Size Example: Slope II
  • Class Size Example: Slope III
  • Class Size Example: Slope and Average Effect
  • Class Size Example: Marginal Effect
  • Econometric Models: Overview I
  • Econometric Models: Overview II
  • The Population Regression Model
  • Deriving OLS Estimators
  • Actual, Predicted, and Residual Values
  • Actual, Predicted, and Residual Values
  • Actual, Predicted, and Residual Values
  • Deriving OLS Estimators
  • Deriving OLS Estimators
  • O-rdinary L-east S-quares Estimators
  • The OLS Regression Line
  • The OLS Regression Estimators
  • (Some) Properties of OLS
  • Our Class Size Example in R
  • Class Size Scatterplot (Again)
  • Class Size Scatterplot with Regression Line
  • Linear Regression in R I
  • Linear Regression in R II
  • Linear Regression in R II
  • Tidy Regression with broom
  • Tidy Regression with broom: tidy()
  • Tidy Regression with broom: tidy()
  • Tidy Regression with broom: glance()
  • Tidy Regression with broom: augment()
  • Class Size Regression Result
  • Class Size Regression Residuals
  • Class Size Regression: Fitted and Residual Values
  • Class Size Regression: An Example Data Point I
  • Class Size Regression: An Example Data Point II
  • Class Size Regression: An Example Data Point III
  • Making Predictions
  • Making Predictions In R
  • Making Predictions In R, Manually I
  • Making Predictions In R, Manually II
  • Making Predictions In R, Manually II
  • f Fullscreen
  • s Speaker View
  • o Slide Overview
  • e PDF Export Mode
  • b Toggle Chalkboard
  • c Toggle Notes Canvas
  • d Download Drawings
  • ? Keyboard Help