2.4 — Goodness of Fit and Bias
ECON 480 • Econometrics • Fall 2022
Dr. Ryan Safner
Associate Professor of Economics
safner@hood.edu
ryansafner/metricsF22
metricsF22.classes.ryansafner.com
Contents
Actual, Predicted, and Residual Values
- With a simple linear regression model, for each associated X value, we have
- The observed (or actual) values of Yi
- Predicted (or fitted) values, ˆYi
- The residual (or error), ˆui=Yi−ˆYi … the difference between predicted and observed values
Yi=ˆYi+ˆuiObservedi=Modeli+Errori
“All models are wrong. But some are useful. — George Box”
Goodness of Fit
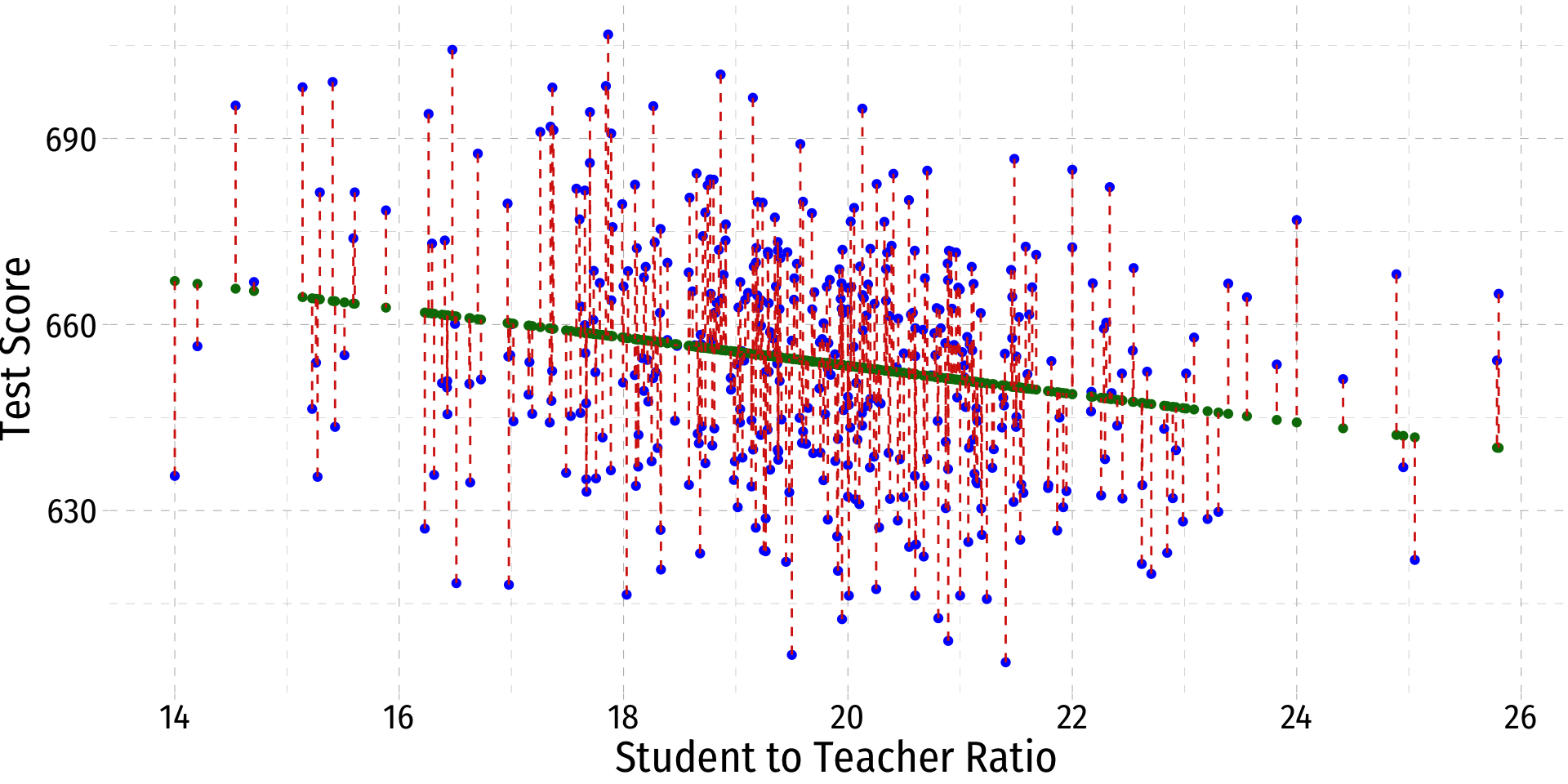
Goodness of Fit
How well does a line fit data? How tightly clustered around the line are the data points?
Quantify how much variation in Yi is “explained” by the model, ˆYi
Yi⏟Observed=ˆYi⏟Model+ˆui⏟Error
- Recall OLS estimators chosen to minimize Sum of Squared Residuals (SSR): (n∑i=1^ui2)
R2
- Primary measure1 is R-squared, the fraction of variation in Yi explained by variation in predicted values ˆYi
R2=var(ˆYi)var(Yi)
R2 Formula I
R2=SSMSST
- Model Sum of Squares (SSM):1 sum of squared deviations of predicted values from their mean2
SSM=n∑i=1(^Yi−ˉY)2
- Total Sum of Squares (TSS): sum of squared deviations of observed values from their mean
SST=n∑i=1(Yi−ˉY)2
R2 Formula II
- Equivalently, R2 is the complement of the fraction of unexplained variation in Yi
R2=1−(SSRSST)
- Equivalently, the square of the correlation coefficient between X and Y1:
R2=(rX,Y)2
Visualizing R2 I
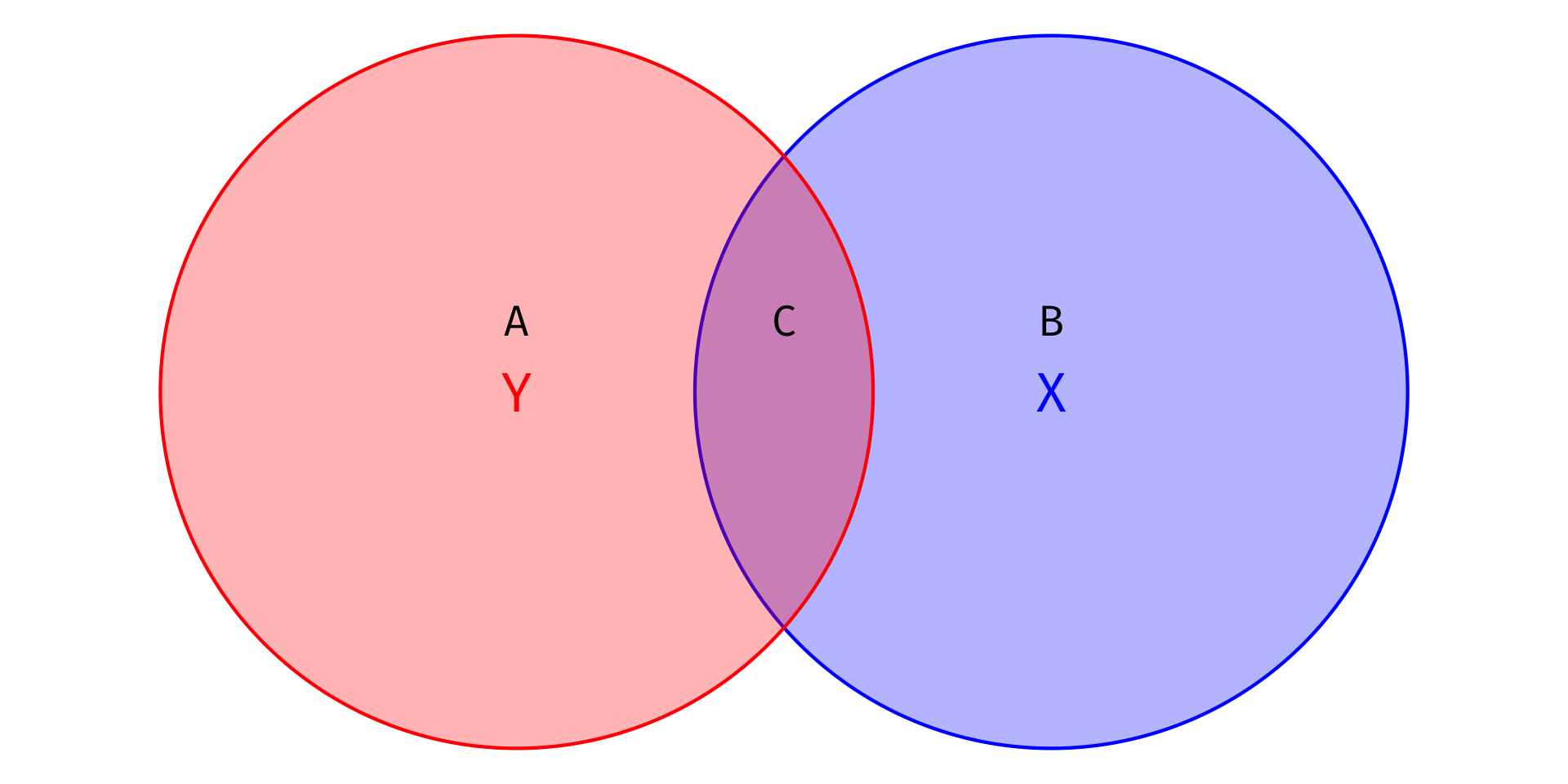
- Total Variation in Y: Areas A + C
SST=n∑i=1(Yi−ˉY)2
- Variation in Y explained by X: Area C
SSM=n∑i=1(^Yi−ˉY)2
- Unexplained variation in Y: Area A
SSR=n∑i=1(^ui)2
R2=SSMSST=CA+C
Visualizing R2 II
# make a function to calc. sum of sq. devs
sum_sq <- function(x){sum((x - mean(x))^2)}
# find total sum of squares
SST <- school_reg %>%
augment() %>%
summarize(SST = sum_sq(testscr))
# find explained sum of squares
SSM <- school_reg %>%
augment() %>%
summarize(SSM = sum_sq(.fitted))
# look at them and divide to get R^2
tribble(
~SSM, ~SST, ~R_sq,
SSM, SST, SSM/SST
) %>%
knitr::kable()| SSM | SST | R_sq |
|---|---|---|
| 7794.11 | 152109.6 | 0.0512401 |
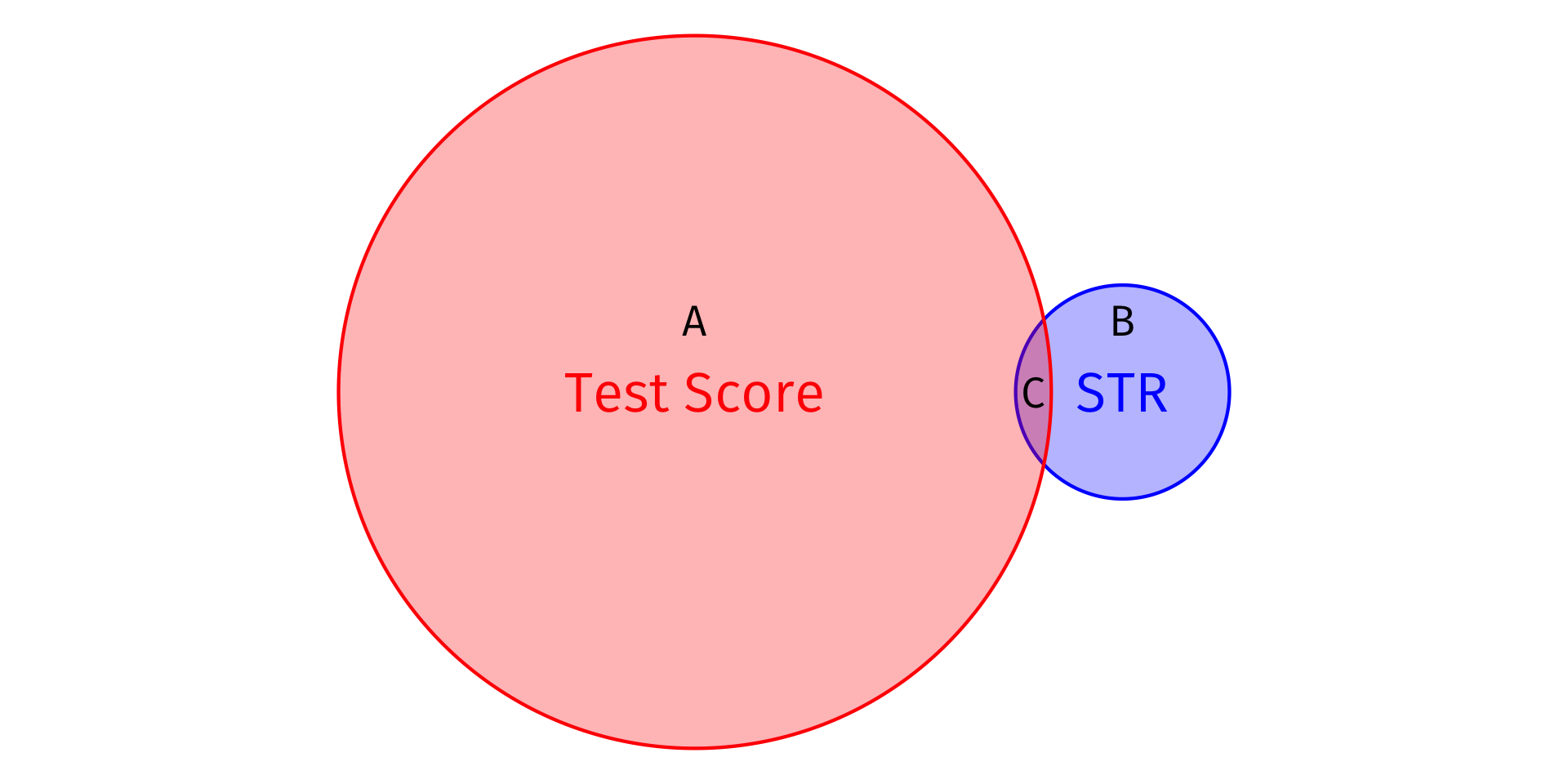
R2=SSMSST=CA+C=0.05
Calculating R2 in R I
- Recall
broom’saugment()command makes a lot of new regression-based values like:.fitted: predicted values (^Yi).resid: residuals (^ui)
| testscr | str | .fitted | .resid | .hat | .sigma | .cooksd | .std.resid |
|---|---|---|---|---|---|---|---|
| 690.80 | 17.88991 | 658.1474 | 32.6526000 | 0.0044244 | 18.53408 | 0.0068925 | 1.7612148 |
| 661.20 | 21.52466 | 649.8608 | 11.3391671 | 0.0047485 | 18.59490 | 0.0008927 | 0.6117112 |
| 643.60 | 18.69723 | 656.3069 | -12.7068869 | 0.0029742 | 18.59279 | 0.0006996 | -0.6848850 |
| 647.70 | 17.35714 | 659.3620 | -11.6619808 | 0.0058575 | 18.59441 | 0.0011673 | -0.6294767 |
| 640.85 | 18.67133 | 656.3659 | -15.5159250 | 0.0030072 | 18.58766 | 0.0010548 | -0.8363024 |
| 605.55 | 21.40625 | 650.1308 | -44.5807574 | 0.0044603 | 18.47411 | 0.0129531 | -2.4046387 |
| 606.75 | 19.50000 | 654.4767 | -47.7266907 | 0.0023941 | 18.45548 | 0.0079356 | -2.5716597 |
| 609.00 | 20.89412 | 651.2984 | -42.2983704 | 0.0034291 | 18.48716 | 0.0089463 | -2.2803484 |
| 612.50 | 19.94737 | 653.4568 | -40.9567760 | 0.0024438 | 18.49453 | 0.0059658 | -2.2069310 |
| 612.65 | 20.80556 | 651.5003 | -38.8502504 | 0.0032862 | 18.50537 | 0.0072306 | -2.0943066 |
| 615.75 | 21.23809 | 650.5142 | -34.7641689 | 0.0040831 | 18.52485 | 0.0072052 | -1.8747872 |
| 616.30 | 21.00000 | 651.0570 | -34.7569905 | 0.0036136 | 18.52492 | 0.0063680 | -1.8739584 |
| 616.30 | 20.60000 | 651.9689 | -35.6689130 | 0.0029950 | 18.52080 | 0.0055515 | -1.9225289 |
| 616.30 | 20.00822 | 653.3181 | -37.0180659 | 0.0024712 | 18.51448 | 0.0049285 | -1.9947233 |
| 616.45 | 18.02778 | 657.8331 | -41.3830610 | 0.0041152 | 18.49207 | 0.0102908 | -2.2317715 |
| 617.35 | 20.25196 | 652.7624 | -35.4123888 | 0.0026303 | 18.52202 | 0.0048022 | -1.9083535 |
| 618.05 | 16.97787 | 660.2267 | -42.1766170 | 0.0071084 | 18.48740 | 0.0185757 | -2.2779936 |
| 618.30 | 16.50980 | 661.2938 | -42.9937160 | 0.0089166 | 18.48263 | 0.0243010 | -2.3242432 |
| 619.80 | 22.70402 | 647.1721 | -27.3721439 | 0.0086398 | 18.55446 | 0.0095387 | -1.4795333 |
| 620.30 | 19.91111 | 653.5394 | -33.2394468 | 0.0024298 | 18.53171 | 0.0039069 | -1.7910748 |
| 620.50 | 18.33333 | 657.1365 | -36.6364656 | 0.0035203 | 18.51621 | 0.0068913 | -1.9751997 |
| 621.40 | 22.61905 | 647.3659 | -25.9658367 | 0.0082974 | 18.55936 | 0.0082379 | -1.4032766 |
| 621.75 | 19.44828 | 654.5946 | -32.8446103 | 0.0024056 | 18.53340 | 0.0037763 | -1.7697780 |
| 622.05 | 25.05263 | 641.8178 | -19.7677069 | 0.0219144 | 18.57747 | 0.0129635 | -1.0757207 |
| 622.60 | 20.67544 | 651.7969 | -29.1969420 | 0.0030953 | 18.54804 | 0.0038451 | -1.5737735 |
| 623.10 | 18.68235 | 656.3408 | -33.2407957 | 0.0029931 | 18.53166 | 0.0048183 | -1.7916534 |
| 623.20 | 22.84553 | 646.8495 | -23.6495125 | 0.0092313 | 18.56681 | 0.0076172 | -1.2786973 |
| 623.45 | 19.26667 | 655.0086 | -31.5586344 | 0.0024741 | 18.53877 | 0.0035862 | -1.7005437 |
| 623.60 | 19.25000 | 655.0466 | -31.4466672 | 0.0024826 | 18.53923 | 0.0035731 | -1.6945175 |
| 624.15 | 20.54545 | 652.0933 | -27.9432316 | 0.0029272 | 18.55269 | 0.0033295 | -1.5060690 |
| 624.55 | 20.60697 | 651.9530 | -27.4029716 | 0.0030039 | 18.55462 | 0.0032865 | -1.4770072 |
| 624.95 | 21.07268 | 650.8913 | -25.9412664 | 0.0037489 | 18.55965 | 0.0036811 | -1.3987447 |
| 625.30 | 21.53581 | 649.8354 | -24.5354367 | 0.0047766 | 18.56421 | 0.0042044 | -1.3236257 |
| 625.85 | 19.90400 | 653.5556 | -27.7056741 | 0.0024273 | 18.55357 | 0.0027114 | -1.4928911 |
| 626.10 | 21.19407 | 650.6145 | -24.5145628 | 0.0039906 | 18.56430 | 0.0035010 | -1.3219776 |
| 626.80 | 21.86535 | 649.0841 | -22.2840870 | 0.0056821 | 18.57102 | 0.0041331 | -1.2027182 |
| 626.90 | 18.32965 | 657.1449 | -30.2448510 | 0.0035267 | 18.54397 | 0.0047052 | -1.6306107 |
| 627.10 | 16.22857 | 661.9349 | -34.8349462 | 0.0101436 | 18.52405 | 0.0181933 | -1.8843463 |
| 627.25 | 19.17857 | 655.2095 | -27.9594856 | 0.0025232 | 18.55265 | 0.0028710 | -1.5066399 |
| 627.30 | 20.27737 | 652.7044 | -25.4044560 | 0.0026515 | 18.56148 | 0.0024914 | -1.3690462 |
| 628.25 | 22.98614 | 646.5290 | -18.2789658 | 0.0098456 | 18.58147 | 0.0048593 | -0.9886255 |
| 628.40 | 20.44444 | 652.3235 | -23.9235136 | 0.0028120 | 18.56620 | 0.0023440 | -1.2893420 |
| 628.55 | 19.82085 | 653.7452 | -25.1951733 | 0.0024027 | 18.56217 | 0.0022195 | -1.3575986 |
| 628.65 | 23.20522 | 646.0295 | -17.3794680 | 0.0108552 | 18.58354 | 0.0048531 | -0.9404554 |
| 628.75 | 19.26697 | 655.0080 | -26.2579595 | 0.0024740 | 18.55863 | 0.0024826 | -1.4149156 |
| 629.80 | 23.30189 | 645.8091 | -16.0090672 | 0.0113210 | 18.58652 | 0.0042987 | -0.8665030 |
| 630.35 | 21.18829 | 650.6277 | -20.2777471 | 0.0039786 | 18.57661 | 0.0023882 | -1.0934956 |
| 630.40 | 20.87180 | 651.3493 | -20.9492352 | 0.0033921 | 18.57483 | 0.0021706 | -1.1293737 |
| 630.55 | 19.01749 | 655.5767 | -25.0267237 | 0.0026397 | 18.56271 | 0.0024071 | -1.3486822 |
| 630.55 | 21.91938 | 648.9610 | -18.4109799 | 0.0058443 | 18.58124 | 0.0029028 | -0.9937597 |
| 631.05 | 20.10124 | 653.1060 | -22.0559340 | 0.0025226 | 18.57177 | 0.0017862 | -1.1885175 |
| 631.40 | 21.47651 | 649.9706 | -18.5706002 | 0.0046291 | 18.58089 | 0.0023335 | -1.0017633 |
| 631.85 | 20.06579 | 653.1868 | -21.3368264 | 0.0025016 | 18.57379 | 0.0016576 | -1.1497552 |
| 631.90 | 20.37510 | 652.4816 | -20.5816166 | 0.0027409 | 18.57584 | 0.0016907 | -1.1091931 |
| 631.95 | 22.44648 | 647.7593 | -15.8092651 | 0.0076317 | 18.58699 | 0.0028050 | -0.8540965 |
| 632.00 | 22.89524 | 646.7362 | -14.7361970 | 0.0094455 | 18.58910 | 0.0030274 | -0.7968524 |
| 632.20 | 20.49797 | 652.2015 | -20.0014969 | 0.0028713 | 18.57736 | 0.0016732 | -1.0779995 |
| 632.25 | 20.00000 | 653.3368 | -21.0867866 | 0.0024672 | 18.57448 | 0.0015966 | -1.1362620 |
| 632.45 | 22.25658 | 648.1922 | -15.7422648 | 0.0069451 | 18.58714 | 0.0025275 | -0.8501827 |
| 632.85 | 21.56436 | 649.7703 | -16.9203622 | 0.0048493 | 18.58468 | 0.0020303 | -0.9128447 |
| 632.95 | 19.47737 | 654.5283 | -21.5782678 | 0.0023987 | 18.57313 | 0.0016253 | -1.1627056 |
| 633.05 | 17.67002 | 658.6487 | -25.5987041 | 0.0049700 | 18.56074 | 0.0047638 | -1.3811205 |
| 633.15 | 21.94756 | 648.8967 | -15.7466959 | 0.0059305 | 18.58715 | 0.0021551 | -0.8499879 |
| 633.65 | 21.78339 | 649.2710 | -15.6209661 | 0.0054434 | 18.58741 | 0.0019447 | -0.8429946 |
| 633.90 | 19.14000 | 655.2974 | -21.3973987 | 0.0025479 | 18.57362 | 0.0016981 | -1.1530460 |
| 634.00 | 18.11050 | 657.6445 | -23.6444923 | 0.0039418 | 18.56702 | 0.0032168 | -1.2750268 |
| 634.05 | 20.68242 | 651.7810 | -17.7309406 | 0.0031050 | 18.58290 | 0.0014225 | -0.9557378 |
| 634.10 | 22.62361 | 647.3555 | -13.2554886 | 0.0083155 | 18.59181 | 0.0021516 | -0.7163754 |
| 634.10 | 21.78650 | 649.2639 | -15.1639357 | 0.0054522 | 18.58833 | 0.0018356 | -0.8183344 |
| 634.15 | 18.58293 | 656.5674 | -22.4174066 | 0.0031267 | 18.57071 | 0.0022899 | -1.2083620 |
| 634.20 | 21.54545 | 649.8134 | -15.6134965 | 0.0048011 | 18.58744 | 0.0017114 | -0.8423196 |
| 634.40 | 21.15289 | 650.7084 | -16.3083914 | 0.0039064 | 18.58602 | 0.0015165 | -0.8794127 |
| 634.55 | 16.63333 | 661.0121 | -26.4621537 | 0.0084110 | 18.55766 | 0.0086750 | -1.4301811 |
| 634.70 | 21.14438 | 650.7278 | -16.0278017 | 0.0038893 | 18.58660 | 0.0014583 | -0.8642748 |
| 634.90 | 19.78182 | 653.8342 | -18.9341744 | 0.0023943 | 18.58006 | 0.0012491 | -1.0202312 |
| 634.95 | 18.98373 | 655.6537 | -20.7037398 | 0.0026685 | 18.57551 | 0.0016654 | -1.1157341 |
| 635.05 | 17.66767 | 658.6541 | -23.6040700 | 0.0049762 | 18.56711 | 0.0040554 | -1.2735085 |
| 635.20 | 17.75499 | 658.4550 | -23.2550243 | 0.0047515 | 18.56818 | 0.0037570 | -1.2545348 |
| 635.45 | 15.27273 | 664.1141 | -28.6640505 | 0.0151024 | 18.54939 | 0.0185256 | -1.5544390 |
| 635.60 | 14.00000 | 667.0156 | -31.4156607 | 0.0235965 | 18.53797 | 0.0353765 | -1.7110520 |
| 635.60 | 20.59613 | 651.9777 | -16.3777393 | 0.0029900 | 18.58589 | 0.0011685 | -0.8827463 |
| 635.75 | 16.31169 | 661.7454 | -25.9954321 | 0.0097700 | 18.55920 | 0.0097510 | -1.4059202 |
| 635.95 | 21.12796 | 650.7652 | -14.8152370 | 0.0038565 | 18.58903 | 0.0012354 | -0.7988759 |
| 636.10 | 17.48801 | 659.0636 | -22.9636613 | 0.0054704 | 18.56903 | 0.0042238 | -1.2392643 |
| 636.50 | 17.88679 | 658.1545 | -21.6544931 | 0.0044317 | 18.57285 | 0.0030364 | -1.1680036 |
| 636.60 | 19.30676 | 654.9172 | -18.3172679 | 0.0024552 | 18.58154 | 0.0011989 | -0.9870205 |
| 636.70 | 20.89231 | 651.3025 | -14.6025459 | 0.0034261 | 18.58944 | 0.0010653 | -0.7872370 |
| 636.90 | 21.28684 | 650.4030 | -13.5030170 | 0.0041886 | 18.59143 | 0.0011153 | -0.7282390 |
| 636.95 | 20.19560 | 652.8909 | -15.9408471 | 0.0025865 | 18.58681 | 0.0009568 | -0.8590243 |
| 637.00 | 24.95000 | 642.0517 | -5.0517338 | 0.0211806 | 18.60155 | 0.0008170 | -0.2748026 |
| 637.10 | 18.13043 | 657.5990 | -20.4990630 | 0.0039014 | 18.57602 | 0.0023929 | -1.1053874 |
| 637.35 | 20.00000 | 653.3368 | -15.9868110 | 0.0024672 | 18.58671 | 0.0009177 | -0.8614497 |
| 637.65 | 18.72951 | 656.2333 | -18.5832373 | 0.0029343 | 18.58090 | 0.0014762 | -1.0015927 |
| 637.95 | 18.25000 | 657.3265 | -19.3764999 | 0.0036702 | 18.57893 | 0.0020103 | -1.0447333 |
| 637.95 | 18.99257 | 655.6335 | -17.6835240 | 0.0026608 | 18.58301 | 0.0012114 | -0.9529696 |
| 638.00 | 19.88764 | 653.5929 | -15.5929415 | 0.0024217 | 18.58752 | 0.0008569 | -0.8402069 |
| 638.20 | 19.37895 | 654.7527 | -16.5526534 | 0.0024265 | 18.58552 | 0.0009675 | -0.8919220 |
| 638.30 | 20.46259 | 652.2822 | -13.9821316 | 0.0028317 | 18.59059 | 0.0008063 | -0.7535652 |
| 638.30 | 22.29157 | 648.1124 | -9.8123916 | 0.0070680 | 18.59698 | 0.0009996 | -0.5299645 |
| 638.35 | 20.70474 | 651.7301 | -13.3801421 | 0.0031363 | 18.59165 | 0.0008183 | -0.7212312 |
| 638.55 | 19.06005 | 655.4797 | -16.9296980 | 0.0026056 | 18.58470 | 0.0010872 | -0.9123205 |
| 638.70 | 20.23247 | 652.8068 | -14.1067884 | 0.0026147 | 18.59037 | 0.0007575 | -0.7602008 |
| 639.25 | 19.69012 | 654.0432 | -14.7932476 | 0.0023826 | 18.58909 | 0.0007587 | -0.7971007 |
| 639.30 | 20.36254 | 652.5103 | -13.2102177 | 0.0027287 | 18.59195 | 0.0006934 | -0.7119262 |
| 639.35 | 19.75422 | 653.8971 | -14.5471357 | 0.0023896 | 18.58956 | 0.0007359 | -0.7838423 |
| 639.50 | 19.37977 | 654.7508 | -15.2508001 | 0.0024263 | 18.58820 | 0.0008212 | -0.8217729 |
| 639.75 | 22.92351 | 646.6717 | -6.9217452 | 0.0095687 | 18.60012 | 0.0006768 | -0.3743132 |
| 639.80 | 19.37340 | 654.7653 | -14.9653316 | 0.0024285 | 18.58876 | 0.0007915 | -0.8063916 |
| 639.85 | 19.15516 | 655.2629 | -15.4128952 | 0.0025380 | 18.58788 | 0.0008776 | -0.8305537 |
| 639.90 | 21.30000 | 650.3730 | -10.4730131 | 0.0042176 | 18.59613 | 0.0006756 | -0.5648343 |
| 640.10 | 18.30357 | 657.2043 | -17.1043423 | 0.0035727 | 18.58430 | 0.0015246 | -0.9221791 |
| 640.15 | 21.07926 | 650.8763 | -10.7262653 | 0.0037615 | 18.59579 | 0.0006315 | -0.5783604 |
| 640.50 | 18.79121 | 656.0926 | -15.5926000 | 0.0028619 | 18.58751 | 0.0010135 | -0.8403739 |
| 640.75 | 19.62662 | 654.1880 | -13.4380273 | 0.0023811 | 18.59156 | 0.0006257 | -0.7240772 |
| 640.90 | 19.59016 | 654.2711 | -13.3711093 | 0.0023826 | 18.59168 | 0.0006199 | -0.7204720 |
| 641.10 | 20.87187 | 651.3491 | -10.2491101 | 0.0033922 | 18.59644 | 0.0005196 | -0.5525298 |
| 641.45 | 21.11500 | 650.7948 | -9.3448453 | 0.0038309 | 18.59758 | 0.0004882 | -0.5038918 |
| 641.45 | 20.08452 | 653.1441 | -11.6941452 | 0.0025125 | 18.59439 | 0.0005001 | -0.6301536 |
| 641.55 | 19.91049 | 653.5409 | -11.9908687 | 0.0024296 | 18.59394 | 0.0005084 | -0.6461161 |
| 641.80 | 17.81285 | 658.3231 | -16.5230183 | 0.0046083 | 18.58555 | 0.0018389 | -0.8913003 |
| 642.20 | 18.13333 | 657.5924 | -15.3924778 | 0.0038956 | 18.58790 | 0.0013471 | -0.8300185 |
| 642.20 | 19.22221 | 655.1100 | -12.9099823 | 0.0024976 | 18.59246 | 0.0006059 | -0.6956653 |
| 642.40 | 18.66072 | 656.3901 | -13.9900750 | 0.0030210 | 18.59058 | 0.0008615 | -0.7540649 |
| 642.75 | 19.60000 | 654.2487 | -11.4987090 | 0.0023820 | 18.59469 | 0.0004583 | -0.6195818 |
| 643.05 | 19.28384 | 654.9695 | -11.9195015 | 0.0024657 | 18.59405 | 0.0005098 | -0.6422822 |
| 643.20 | 22.81818 | 646.9119 | -3.7119208 | 0.0091149 | 18.60234 | 0.0001852 | -0.2006868 |
| 643.25 | 18.80922 | 656.0515 | -12.8015382 | 0.0028417 | 18.59264 | 0.0006783 | -0.6899407 |
| 643.40 | 21.37363 | 650.2052 | -6.8051436 | 0.0043842 | 18.60024 | 0.0002966 | -0.3670482 |
| 643.40 | 20.02041 | 653.2903 | -9.8902344 | 0.0024772 | 18.59691 | 0.0003527 | -0.5329382 |
| 643.50 | 21.49862 | 649.9202 | -6.4202311 | 0.0046835 | 18.60056 | 0.0002822 | -0.3463393 |
| 643.50 | 15.42857 | 663.7588 | -20.2587667 | 0.0142107 | 18.57638 | 0.0086918 | -1.0981272 |
| 643.70 | 22.40000 | 647.8652 | -4.1652964 | 0.0074592 | 18.60211 | 0.0001902 | -0.2250108 |
| 643.70 | 20.12709 | 653.0471 | -9.3470412 | 0.0025389 | 18.59759 | 0.0003229 | -0.5036836 |
| 644.20 | 19.03798 | 655.5300 | -11.3300673 | 0.0026230 | 18.59494 | 0.0004902 | -0.6105686 |
| 644.20 | 17.34216 | 659.3962 | -15.1961460 | 0.0059033 | 18.58826 | 0.0019977 | -0.8202586 |
| 644.40 | 17.01863 | 660.1337 | -15.7337076 | 0.0069648 | 18.58716 | 0.0025321 | -0.8497290 |
| 644.45 | 20.80000 | 651.5129 | -7.0629295 | 0.0032776 | 18.60001 | 0.0002383 | -0.3807408 |
| 644.45 | 21.15385 | 650.7062 | -6.2562250 | 0.0039083 | 18.60070 | 0.0002233 | -0.3373606 |
| 644.50 | 18.45833 | 656.8515 | -12.3514896 | 0.0033128 | 18.59337 | 0.0007368 | -0.6658426 |
| 644.55 | 19.14082 | 655.2955 | -10.7455612 | 0.0025474 | 18.59577 | 0.0004282 | -0.5790481 |
| 644.70 | 19.40766 | 654.6872 | -9.9872625 | 0.0024171 | 18.59679 | 0.0003508 | -0.5381504 |
| 644.95 | 19.56896 | 654.3195 | -9.3694538 | 0.0023844 | 18.59756 | 0.0003046 | -0.5048523 |
| 645.10 | 21.50120 | 649.9143 | -4.8143634 | 0.0046899 | 18.60173 | 0.0001589 | -0.2597116 |
| 645.25 | 17.52941 | 658.9693 | -13.7192551 | 0.0053527 | 18.59103 | 0.0014748 | -0.7403339 |
| 645.55 | 16.43017 | 661.4753 | -15.9253223 | 0.0092534 | 18.58673 | 0.0034625 | -0.8610703 |
| 645.55 | 19.79654 | 653.8006 | -8.2505891 | 0.0023972 | 18.59883 | 0.0002375 | -0.4445676 |
| 645.60 | 17.18613 | 659.7519 | -14.1518853 | 0.0063978 | 18.59024 | 0.0018796 | -0.7640815 |
| 645.75 | 17.61589 | 658.7721 | -13.0220905 | 0.0051142 | 18.59224 | 0.0012689 | -0.7026285 |
| 645.75 | 20.12537 | 653.0510 | -7.3009626 | 0.0025378 | 18.59979 | 0.0001969 | -0.3934265 |
| 646.00 | 22.16667 | 648.3972 | -2.3972034 | 0.0066367 | 18.60286 | 0.0000560 | -0.1294442 |
| 646.20 | 19.96154 | 653.4245 | -7.2244596 | 0.0024497 | 18.59986 | 0.0001861 | -0.3892868 |
| 646.35 | 19.03945 | 655.5267 | -9.1766772 | 0.0026218 | 18.59779 | 0.0003214 | -0.4945238 |
| 646.40 | 15.22436 | 664.2243 | -17.8243069 | 0.0153857 | 18.58242 | 0.0073020 | -0.9667435 |
| 646.50 | 21.14475 | 650.7270 | -4.2269747 | 0.0038900 | 18.60208 | 0.0001014 | -0.2279332 |
| 646.55 | 19.64390 | 654.1486 | -7.5986387 | 0.0023810 | 18.59950 | 0.0002000 | -0.4094351 |
| 646.70 | 21.04869 | 650.9460 | -4.2459648 | 0.0037035 | 18.60207 | 0.0000974 | -0.2289358 |
| 646.90 | 20.17544 | 652.9368 | -6.0367973 | 0.0025718 | 18.60088 | 0.0001364 | -0.3253100 |
| 646.95 | 21.39130 | 650.1649 | -3.2149290 | 0.0044252 | 18.60256 | 0.0000668 | -0.1734068 |
| 647.05 | 20.00833 | 653.3178 | -6.2678181 | 0.0024712 | 18.60070 | 0.0001413 | -0.3377422 |
| 647.25 | 20.29137 | 652.6725 | -5.4225136 | 0.0026635 | 18.60133 | 0.0001140 | -0.2922210 |
| 647.30 | 17.66667 | 658.6563 | -11.3563529 | 0.0049788 | 18.59488 | 0.0009392 | -0.6127092 |
| 647.60 | 18.22055 | 657.3936 | -9.7936146 | 0.0037254 | 18.59703 | 0.0005213 | -0.5280623 |
| 647.60 | 20.27100 | 652.7190 | -5.1189788 | 0.0026461 | 18.60154 | 0.0001010 | -0.2758610 |
| 648.00 | 20.19895 | 652.8832 | -4.8832278 | 0.0025890 | 18.60169 | 0.0000899 | -0.2631489 |
| 648.20 | 21.38424 | 650.1810 | -1.9809613 | 0.0044088 | 18.60298 | 0.0000253 | -0.1068482 |
| 648.25 | 20.97368 | 651.1170 | -2.8669730 | 0.0035663 | 18.60270 | 0.0000428 | -0.1545721 |
| 648.35 | 20.00000 | 653.3368 | -4.9868110 | 0.0024672 | 18.60163 | 0.0000893 | -0.2687144 |
| 648.70 | 17.15328 | 659.8268 | -11.1267409 | 0.0065060 | 18.59520 | 0.0011818 | -0.6007822 |
| 648.95 | 22.34977 | 647.9798 | 0.9701931 | 0.0072760 | 18.60317 | 0.0000101 | 0.0524053 |
| 649.15 | 22.17007 | 648.3894 | 0.7605829 | 0.0066482 | 18.60320 | 0.0000056 | 0.0410702 |
| 649.30 | 18.18182 | 657.4819 | -8.1818441 | 0.0037997 | 18.59890 | 0.0003712 | -0.4411736 |
| 649.50 | 18.95714 | 655.7143 | -6.2142988 | 0.0026923 | 18.60074 | 0.0001514 | -0.3348954 |
| 649.70 | 19.74533 | 653.9174 | -4.2174323 | 0.0023883 | 18.60208 | 0.0000618 | -0.2272475 |
| 649.85 | 16.42623 | 661.4843 | -11.6343227 | 0.0092702 | 18.59443 | 0.0018514 | -0.6290645 |
| 650.45 | 16.62540 | 661.0302 | -10.5802839 | 0.0084429 | 18.59596 | 0.0013921 | -0.5718342 |
| 650.55 | 16.38177 | 661.5857 | -11.0356758 | 0.0094622 | 18.59531 | 0.0017009 | -0.5967536 |
| 650.60 | 20.07416 | 653.1677 | -2.5677456 | 0.0025064 | 18.60281 | 0.0000241 | -0.1383658 |
| 650.65 | 17.99544 | 657.9068 | -7.2567670 | 0.0041854 | 18.59982 | 0.0003219 | -0.3913683 |
| 650.90 | 19.39130 | 654.7245 | -3.8244723 | 0.0024223 | 18.60229 | 0.0000516 | -0.2060772 |
| 650.90 | 16.42857 | 661.4790 | -10.5789340 | 0.0092602 | 18.59595 | 0.0015290 | -0.5719970 |
| 651.15 | 16.72949 | 660.7929 | -9.6429060 | 0.0080316 | 18.59719 | 0.0010991 | -0.5210635 |
| 651.20 | 24.41345 | 643.2750 | 7.9250504 | 0.0175731 | 18.59911 | 0.0016561 | 0.4303121 |
| 651.35 | 18.26415 | 657.2942 | -5.9442148 | 0.0036441 | 18.60095 | 0.0001878 | -0.3204933 |
| 651.40 | 18.95504 | 655.7191 | -4.3190663 | 0.0026942 | 18.60203 | 0.0000732 | -0.2327595 |
| 651.45 | 21.03896 | 650.9682 | 0.4818585 | 0.0036853 | 18.60322 | 0.0000012 | 0.0259808 |
| 651.80 | 20.74074 | 651.6480 | 0.1520070 | 0.0031883 | 18.60323 | 0.0000001 | 0.0081939 |
| 651.85 | 18.10000 | 657.6684 | -5.8184459 | 0.0039633 | 18.60104 | 0.0001959 | -0.3137625 |
| 651.90 | 19.84615 | 653.6875 | -1.7875032 | 0.0024092 | 18.60303 | 0.0000112 | -0.0963169 |
| 652.00 | 21.60000 | 649.6891 | 2.3109075 | 0.0049416 | 18.60289 | 0.0000386 | 0.1246780 |
| 652.10 | 22.44242 | 647.7685 | 4.3314405 | 0.0076165 | 18.60201 | 0.0002101 | 0.2340045 |
| 652.10 | 23.01438 | 646.4646 | 5.6353877 | 0.0099721 | 18.60117 | 0.0004679 | 0.3048118 |
| 652.30 | 17.74892 | 658.4688 | -6.1688330 | 0.0047668 | 18.60077 | 0.0002652 | -0.3327915 |
| 652.30 | 18.28664 | 657.2429 | -4.9428697 | 0.0036031 | 18.60165 | 0.0001284 | -0.2664984 |
| 652.35 | 19.26544 | 655.0114 | -2.6614627 | 0.0024747 | 18.60278 | 0.0000255 | -0.1434135 |
| 652.40 | 22.66667 | 647.2573 | 5.1427251 | 0.0084881 | 18.60151 | 0.0003307 | 0.2779560 |
| 652.40 | 19.29412 | 654.9461 | -2.5460401 | 0.0024609 | 18.60281 | 0.0000232 | -0.1371930 |
| 652.50 | 17.36364 | 659.3472 | -6.8471910 | 0.0058378 | 18.60019 | 0.0004010 | -0.3695860 |
| 652.85 | 19.82143 | 653.7439 | -0.8939202 | 0.0024028 | 18.60318 | 0.0000028 | -0.0481674 |
| 653.10 | 20.43378 | 652.3479 | 0.7521214 | 0.0028007 | 18.60320 | 0.0000023 | 0.0405349 |
| 653.40 | 21.03721 | 650.9721 | 2.4278745 | 0.0036820 | 18.60285 | 0.0000317 | 0.1309058 |
| 653.50 | 19.92462 | 653.5086 | -0.0086306 | 0.0024348 | 18.60323 | 0.0000000 | -0.0004651 |
| 653.55 | 19.00986 | 655.5941 | -2.0441346 | 0.0026461 | 18.60296 | 0.0000161 | -0.1101581 |
| 653.55 | 23.82222 | 644.6229 | 8.9271951 | 0.0140425 | 18.59802 | 0.0016672 | 0.4838576 |
| 653.70 | 19.36909 | 654.7752 | -1.0751999 | 0.0024300 | 18.60316 | 0.0000041 | -0.0579361 |
| 653.80 | 19.82857 | 653.7276 | 0.0723767 | 0.0024046 | 18.60323 | 0.0000000 | 0.0038999 |
| 653.85 | 15.25885 | 664.1457 | -10.2957130 | 0.0151833 | 18.59629 | 0.0024033 | -0.5583550 |
| 653.95 | 17.16129 | 659.8085 | -5.8585474 | 0.0064795 | 18.60101 | 0.0003263 | -0.3163248 |
| 654.10 | 21.81333 | 649.2027 | 4.8972418 | 0.0055295 | 18.60168 | 0.0001942 | 0.2642940 |
| 654.20 | 19.07471 | 655.4463 | -1.2463129 | 0.0025944 | 18.60313 | 0.0000059 | -0.0671619 |
| 654.20 | 25.78512 | 640.1478 | 14.0521378 | 0.0275595 | 18.59014 | 0.0083342 | 0.7669068 |
| 654.30 | 18.21261 | 657.4117 | -3.1116961 | 0.0037404 | 18.60261 | 0.0000528 | -0.1677809 |
| 654.60 | 18.16606 | 657.5178 | -2.9178351 | 0.0038305 | 18.60268 | 0.0000476 | -0.1573352 |
| 654.85 | 16.97297 | 660.2378 | -5.3878525 | 0.0071258 | 18.60135 | 0.0003039 | -0.2910049 |
| 654.85 | 21.50087 | 649.9151 | 4.9348930 | 0.0046891 | 18.60166 | 0.0001669 | 0.2662135 |
| 654.90 | 20.60000 | 651.9689 | 2.9311237 | 0.0029950 | 18.60268 | 0.0000375 | 0.1579855 |
| 655.05 | 16.99029 | 660.1983 | -5.1483570 | 0.0070644 | 18.60151 | 0.0002750 | -0.2780608 |
| 655.05 | 20.77954 | 651.5596 | 3.4904750 | 0.0032463 | 18.60245 | 0.0000577 | 0.1881578 |
| 655.05 | 15.51247 | 663.5675 | -8.5174540 | 0.0137442 | 18.59849 | 0.0014845 | -0.4615797 |
| 655.20 | 19.88506 | 653.5988 | 1.6011176 | 0.0024209 | 18.60307 | 0.0000090 | 0.0862743 |
| 655.30 | 21.39882 | 650.1477 | 5.1523100 | 0.0044428 | 18.60151 | 0.0001723 | 0.2779077 |
| 655.35 | 20.49751 | 652.2026 | 3.1474228 | 0.0028708 | 18.60259 | 0.0000414 | 0.1696333 |
| 655.35 | 19.36376 | 654.7873 | 0.5626794 | 0.0024320 | 18.60321 | 0.0000011 | 0.0303195 |
| 655.40 | 17.65957 | 658.6725 | -3.2724836 | 0.0049975 | 18.60254 | 0.0000783 | -0.1765619 |
| 655.55 | 21.01796 | 651.0160 | 4.5339452 | 0.0036464 | 18.60190 | 0.0001094 | 0.2444563 |
| 655.70 | 19.05565 | 655.4897 | 0.2102249 | 0.0026090 | 18.60323 | 0.0000002 | 0.0113288 |
| 655.80 | 22.53846 | 647.5496 | 8.2504072 | 0.0079816 | 18.59881 | 0.0007995 | 0.4458073 |
| 655.85 | 21.10787 | 650.8111 | 5.0389248 | 0.0038170 | 18.60159 | 0.0001414 | 0.2717065 |
| 656.40 | 20.05135 | 653.2197 | 3.1803139 | 0.0024936 | 18.60258 | 0.0000367 | 0.1713736 |
| 656.50 | 14.20176 | 666.5557 | -10.0556550 | 0.0221058 | 18.59657 | 0.0033851 | -0.5472630 |
| 656.55 | 18.47687 | 656.8092 | -0.2591875 | 0.0032838 | 18.60323 | 0.0000003 | -0.0139720 |
| 656.65 | 18.63542 | 656.4478 | 0.2022480 | 0.0030545 | 18.60323 | 0.0000002 | 0.0109013 |
| 656.70 | 20.94595 | 651.1802 | 5.5198006 | 0.0035175 | 18.60126 | 0.0001563 | 0.2975913 |
| 656.80 | 21.08548 | 650.8621 | 5.9379523 | 0.0037735 | 18.60095 | 0.0001941 | 0.3201764 |
| 656.80 | 18.69288 | 656.3168 | 0.4832807 | 0.0029797 | 18.60322 | 0.0000010 | 0.0260483 |
| 657.00 | 20.86808 | 651.3577 | 5.6422654 | 0.0033860 | 18.60117 | 0.0001572 | 0.3041737 |
| 657.00 | 19.82558 | 653.7344 | 3.2655619 | 0.0024038 | 18.60254 | 0.0000373 | 0.1759593 |
| 657.15 | 19.75000 | 653.9067 | 3.2432858 | 0.0023890 | 18.60255 | 0.0000366 | 0.1747577 |
| 657.40 | 19.50000 | 654.4767 | 2.9233337 | 0.0023941 | 18.60268 | 0.0000298 | 0.1575181 |
| 657.50 | 18.39080 | 657.0054 | 0.4945557 | 0.0034223 | 18.60322 | 0.0000012 | 0.0266619 |
| 657.55 | 18.78676 | 656.1027 | 1.4473171 | 0.0028669 | 18.60310 | 0.0000087 | 0.0780043 |
| 657.65 | 19.77018 | 653.8607 | 3.7892917 | 0.0023922 | 18.60231 | 0.0000500 | 0.2041784 |
| 657.75 | 19.33333 | 654.8567 | 2.8933427 | 0.0024438 | 18.60269 | 0.0000298 | 0.1559060 |
| 657.80 | 21.46392 | 649.9993 | 7.8006508 | 0.0045983 | 18.59929 | 0.0004090 | 0.4207880 |
| 657.90 | 23.08492 | 646.3038 | 11.5962704 | 0.0102929 | 18.59447 | 0.0020464 | 0.6273309 |
| 658.00 | 21.06299 | 650.9134 | 7.0866316 | 0.0037305 | 18.59998 | 0.0002734 | 0.3821053 |
| 658.35 | 18.68687 | 656.3305 | 2.0195013 | 0.0029873 | 18.60297 | 0.0000178 | 0.1088493 |
| 658.60 | 20.77024 | 651.5808 | 7.0191773 | 0.0032322 | 18.60005 | 0.0002321 | 0.3783736 |
| 658.80 | 19.30556 | 654.9200 | 3.8800005 | 0.0024557 | 18.60226 | 0.0000538 | 0.2090727 |
| 659.05 | 20.13280 | 653.0340 | 6.0160275 | 0.0025426 | 18.60089 | 0.0001340 | 0.3241860 |
| 659.15 | 20.66964 | 651.8101 | 7.3398790 | 0.0030873 | 18.59975 | 0.0002424 | 0.3956326 |
| 659.35 | 22.28155 | 648.1353 | 11.2146930 | 0.0070326 | 18.59507 | 0.0012991 | 0.6056916 |
| 659.40 | 20.60027 | 651.9683 | 7.4317411 | 0.0029953 | 18.59966 | 0.0002410 | 0.4005656 |
| 659.40 | 20.82734 | 651.4506 | 7.9494125 | 0.0033204 | 18.59915 | 0.0003059 | 0.4285376 |
| 659.80 | 19.22492 | 655.1038 | 4.6961767 | 0.0024961 | 18.60181 | 0.0000801 | 0.2530573 |
| 659.90 | 17.65477 | 658.6835 | 1.2165628 | 0.0050102 | 18.60314 | 0.0000108 | 0.0656382 |
| 660.05 | 17.00000 | 660.1762 | -0.1261626 | 0.0070301 | 18.60323 | 0.0000002 | -0.0068139 |
| 660.10 | 16.49773 | 661.3213 | -1.2213189 | 0.0089672 | 18.60314 | 0.0000197 | -0.0660263 |
| 660.20 | 19.78261 | 653.8324 | 6.3675526 | 0.0023944 | 18.60061 | 0.0001413 | 0.3431032 |
| 660.30 | 22.30216 | 648.0883 | 12.2116809 | 0.0071055 | 18.59355 | 0.0015566 | 0.6595619 |
| 660.75 | 17.73077 | 658.5102 | 2.2398043 | 0.0048128 | 18.60291 | 0.0000353 | 0.1208341 |
| 660.95 | 20.44836 | 652.3146 | 8.6353404 | 0.0028162 | 18.59841 | 0.0003059 | 0.4653970 |
| 661.35 | 20.37169 | 652.4894 | 8.8605813 | 0.0027376 | 18.59816 | 0.0003130 | 0.4775174 |
| 661.45 | 20.16479 | 652.9611 | 8.4889091 | 0.0025643 | 18.59858 | 0.0002690 | 0.4574473 |
| 661.60 | 21.61538 | 649.6540 | 11.9459398 | 0.0049820 | 18.59399 | 0.0010400 | 0.6445202 |
| 661.60 | 20.56143 | 652.0568 | 9.5431374 | 0.0029466 | 18.59735 | 0.0003909 | 0.5143558 |
| 661.85 | 19.95551 | 653.4382 | 8.4117628 | 0.0024472 | 18.59866 | 0.0002520 | 0.4532635 |
| 661.85 | 21.18387 | 650.6378 | 11.2121864 | 0.0039695 | 18.59510 | 0.0007285 | 0.6046244 |
| 661.85 | 18.81042 | 656.0488 | 5.8011813 | 0.0028404 | 18.60106 | 0.0001392 | 0.3126553 |
| 661.90 | 20.57838 | 652.0182 | 9.8818390 | 0.0029676 | 18.59692 | 0.0004222 | 0.5326168 |
| 661.90 | 18.32461 | 657.1564 | 4.7436649 | 0.0035355 | 18.60178 | 0.0001160 | 0.2557495 |
| 661.95 | 18.82063 | 656.0255 | 5.9244818 | 0.0028291 | 18.60096 | 0.0001446 | 0.3192988 |
| 662.40 | 20.81633 | 651.4757 | 10.9243049 | 0.0033030 | 18.59551 | 0.0005747 | 0.5889032 |
| 662.40 | 20.00000 | 653.3368 | 9.0632378 | 0.0024672 | 18.59793 | 0.0002949 | 0.4883728 |
| 662.45 | 19.68182 | 654.0622 | 8.3878317 | 0.0023821 | 18.59869 | 0.0002439 | 0.4519592 |
| 662.50 | 19.39018 | 654.7271 | 7.7729334 | 0.0024227 | 18.59933 | 0.0002130 | 0.4188354 |
| 662.55 | 20.92732 | 651.2227 | 11.3273708 | 0.0034853 | 18.59493 | 0.0006522 | 0.6106874 |
| 662.55 | 19.94437 | 653.4636 | 9.0864284 | 0.0024426 | 18.59790 | 0.0002935 | 0.4896164 |
| 662.65 | 20.79109 | 651.5332 | 11.1167801 | 0.0032639 | 18.59524 | 0.0005880 | 0.5992673 |
| 662.70 | 19.20354 | 655.1526 | 7.5474470 | 0.0025082 | 18.59955 | 0.0002080 | 0.4067027 |
| 662.75 | 19.02439 | 655.5610 | 7.1890123 | 0.0026340 | 18.59989 | 0.0001982 | 0.3874125 |
| 662.90 | 17.62058 | 658.7614 | 4.1386136 | 0.0051016 | 18.60212 | 0.0001278 | 0.2233043 |
| 663.35 | 20.23715 | 652.7961 | 10.5538547 | 0.0026184 | 18.59603 | 0.0004246 | 0.5687378 |
| 663.45 | 19.29374 | 654.9469 | 8.5030256 | 0.0024611 | 18.59856 | 0.0002590 | 0.4581843 |
| 663.50 | 18.82998 | 656.0042 | 7.4957941 | 0.0028190 | 18.59960 | 0.0002307 | 0.4039823 |
| 663.85 | 20.33949 | 652.5628 | 11.2871675 | 0.0027068 | 18.59500 | 0.0005021 | 0.6082824 |
| 663.85 | 19.22900 | 655.0945 | 8.7554483 | 0.0024938 | 18.59828 | 0.0002782 | 0.4717938 |
| 663.90 | 17.89130 | 658.1442 | 5.7558152 | 0.0044211 | 18.60109 | 0.0002140 | 0.3104565 |
| 664.00 | 19.51881 | 654.4338 | 9.5661931 | 0.0023908 | 18.59732 | 0.0003184 | 0.5154548 |
| 664.00 | 19.08451 | 655.4239 | 8.5760649 | 0.0025870 | 18.59848 | 0.0002770 | 0.4621492 |
| 664.15 | 19.93548 | 653.4839 | 10.6661536 | 0.0024390 | 18.59588 | 0.0004038 | 0.5747378 |
| 664.15 | 18.87326 | 655.9055 | 8.2444791 | 0.0027734 | 18.59884 | 0.0002745 | 0.4443222 |
| 664.30 | 20.14178 | 653.0135 | 11.2864431 | 0.0025486 | 18.59500 | 0.0004726 | 0.6081951 |
| 664.40 | 23.55637 | 645.2289 | 19.1710835 | 0.0126069 | 18.57923 | 0.0068826 | 1.0383250 |
| 664.45 | 21.46479 | 649.9973 | 14.4526014 | 0.0046004 | 18.58970 | 0.0014045 | 0.7796128 |
| 664.70 | 19.19101 | 655.1811 | 9.5188868 | 0.0025156 | 18.59738 | 0.0003318 | 0.5129379 |
| 664.75 | 20.13080 | 653.0386 | 11.7114129 | 0.0025413 | 18.59437 | 0.0005074 | 0.6310932 |
| 664.95 | 25.80000 | 640.1139 | 24.8360509 | 0.0276816 | 18.56230 | 0.0261561 | 1.3555326 |
| 664.95 | 18.77774 | 656.1233 | 8.8267082 | 0.0028772 | 18.59820 | 0.0003265 | 0.4757252 |
| 665.10 | 19.10982 | 655.3662 | 9.7337392 | 0.0025687 | 18.59711 | 0.0003543 | 0.5245295 |
| 665.20 | 19.70109 | 654.0183 | 11.1817591 | 0.0023834 | 18.59515 | 0.0004336 | 0.6025041 |
| 665.35 | 18.61594 | 656.4922 | 8.8578021 | 0.0030809 | 18.59816 | 0.0003522 | 0.4774498 |
| 665.65 | 20.99721 | 651.0633 | 14.5866888 | 0.0036085 | 18.58946 | 0.0011200 | 0.7864541 |
| 665.90 | 20.00000 | 653.3368 | 12.5632378 | 0.0024672 | 18.59303 | 0.0005667 | 0.6769704 |
| 665.95 | 20.98325 | 651.0952 | 14.8548507 | 0.0035834 | 18.58895 | 0.0011534 | 0.8009022 |
| 666.00 | 21.64262 | 649.5919 | 16.4080810 | 0.0050542 | 18.58578 | 0.0019907 | 0.8852986 |
| 666.05 | 20.02967 | 653.2691 | 12.7809101 | 0.0024820 | 18.59268 | 0.0005901 | 0.6887048 |
| 666.10 | 19.81140 | 653.7668 | 12.3332116 | 0.0024004 | 18.59340 | 0.0005313 | 0.6645532 |
| 666.15 | 18.00000 | 657.8964 | 8.2536213 | 0.0041755 | 18.59882 | 0.0004154 | 0.4451279 |
| 666.15 | 19.35811 | 654.8002 | 11.3498483 | 0.0024341 | 18.59491 | 0.0004563 | 0.6115767 |
| 666.45 | 20.17912 | 652.9284 | 13.5215262 | 0.0025745 | 18.59142 | 0.0006852 | 0.7286469 |
| 666.55 | 21.11986 | 650.7837 | 15.7663364 | 0.0038405 | 18.58714 | 0.0013932 | 0.8501548 |
| 666.60 | 23.38974 | 645.6088 | 20.9911376 | 0.0117551 | 18.57447 | 0.0076807 | 1.1364108 |
| 666.65 | 22.18182 | 648.3627 | 18.2873646 | 0.0066879 | 18.58152 | 0.0032829 | 0.9875065 |
| 666.65 | 19.94283 | 653.4671 | 13.1828949 | 0.0024419 | 18.59200 | 0.0006176 | 0.7103516 |
| 666.70 | 17.78826 | 658.3791 | 8.3208116 | 0.0046686 | 18.59875 | 0.0004725 | 0.4488627 |
| 666.85 | 14.70588 | 665.4064 | 1.4436151 | 0.0186186 | 18.60310 | 0.0000583 | 0.0784267 |
| 666.85 | 19.04077 | 655.5237 | 11.3263232 | 0.0026207 | 18.59494 | 0.0004895 | 0.6103662 |
| 667.15 | 20.89195 | 651.3033 | 15.8467229 | 0.0034255 | 18.58699 | 0.0012543 | 0.8543115 |
| 667.20 | 19.83851 | 653.7050 | 13.4949908 | 0.0024071 | 18.59146 | 0.0006379 | 0.7271560 |
| 667.45 | 19.52191 | 654.4267 | 13.0232758 | 0.0023903 | 18.59227 | 0.0005899 | 0.7017325 |
| 667.45 | 20.68622 | 651.7723 | 15.6776717 | 0.0031103 | 18.58734 | 0.0011140 | 0.8450642 |
| 667.60 | 18.18182 | 657.4819 | 10.1180826 | 0.0037997 | 18.59661 | 0.0005677 | 0.5455776 |
| 668.00 | 18.89224 | 655.8623 | 12.1377385 | 0.0027542 | 18.59371 | 0.0005909 | 0.6541365 |
| 668.10 | 24.88889 | 642.1911 | 25.9089194 | 0.0207503 | 18.55900 | 0.0210363 | 1.4090755 |
| 668.40 | 18.58064 | 656.5726 | 11.8273796 | 0.0031299 | 18.59419 | 0.0006381 | 0.6375305 |
| 668.60 | 18.04000 | 657.8052 | 10.7947668 | 0.0040890 | 18.59569 | 0.0006957 | 0.5821497 |
| 668.65 | 17.73399 | 658.5029 | 10.1471688 | 0.0048046 | 18.59656 | 0.0007234 | 0.5474222 |
| 668.80 | 21.45455 | 650.0207 | 18.7792872 | 0.0045756 | 18.58038 | 0.0023584 | 1.0129934 |
| 668.90 | 19.92343 | 653.5114 | 15.3886630 | 0.0024344 | 18.58793 | 0.0008390 | 0.8292048 |
| 668.95 | 20.33942 | 652.5630 | 16.3870389 | 0.0027068 | 18.58587 | 0.0010584 | 0.8831220 |
| 669.10 | 22.54608 | 647.5322 | 21.5677538 | 0.0080111 | 18.57299 | 0.0054843 | 1.1654219 |
| 669.30 | 21.10344 | 650.8211 | 18.4789011 | 0.0038083 | 18.58113 | 0.0018977 | 0.9964061 |
| 669.30 | 18.19743 | 657.4463 | 11.8537387 | 0.0037695 | 18.59414 | 0.0007729 | 0.6391564 |
| 669.35 | 20.10768 | 653.0913 | 16.2586817 | 0.0025265 | 18.58614 | 0.0009721 | 0.8761255 |
| 669.35 | 19.15984 | 655.2522 | 14.0977757 | 0.0025350 | 18.59039 | 0.0007334 | 0.7596848 |
| 669.80 | 19.54545 | 654.3731 | 15.4269235 | 0.0023870 | 18.58785 | 0.0008266 | 0.8312467 |
| 669.85 | 20.88889 | 651.3103 | 18.5396862 | 0.0034204 | 18.58099 | 0.0017143 | 0.9994891 |
| 669.95 | 18.39150 | 657.0039 | 12.9461594 | 0.0034211 | 18.59239 | 0.0008361 | 0.6979379 |
| 670.00 | 19.17990 | 655.2065 | 14.7935495 | 0.0025224 | 18.58909 | 0.0008035 | 0.7971728 |
| 670.70 | 19.39771 | 654.7099 | 15.9900520 | 0.0024202 | 18.58671 | 0.0009005 | 0.8616041 |
| 671.25 | 21.67827 | 649.5106 | 21.7393524 | 0.0051503 | 18.57259 | 0.0035616 | 1.1730041 |
| 671.30 | 19.28889 | 654.9580 | 16.3420043 | 0.0024634 | 18.58597 | 0.0009574 | 0.8805876 |
| 671.60 | 20.34927 | 652.5405 | 19.0594660 | 0.0027160 | 18.57974 | 0.0014366 | 1.0271479 |
| 671.60 | 20.96416 | 651.1387 | 20.4612911 | 0.0035495 | 18.57613 | 0.0021675 | 1.1031558 |
| 671.65 | 19.46039 | 654.5670 | 17.0830307 | 0.0024026 | 18.58437 | 0.0010203 | 0.9204897 |
| 671.70 | 19.28572 | 654.9652 | 16.7347320 | 0.0024649 | 18.58513 | 0.0010046 | 0.9017504 |
| 671.75 | 20.91979 | 651.2398 | 20.5101676 | 0.0034724 | 18.57601 | 0.0021302 | 1.1057482 |
| 671.90 | 20.90021 | 651.2845 | 20.6155514 | 0.0034393 | 18.57573 | 0.0021315 | 1.1114112 |
| 671.90 | 20.59575 | 651.9786 | 19.9214224 | 0.0029895 | 18.57756 | 0.0017285 | 1.0737475 |
| 671.95 | 19.37500 | 654.7617 | 17.1882844 | 0.0024279 | 18.58414 | 0.0010439 | 0.9261729 |
| 672.05 | 19.95122 | 653.4480 | 18.6019998 | 0.0024454 | 18.58086 | 0.0012315 | 1.0023582 |
| 672.05 | 18.84973 | 655.9592 | 16.0908748 | 0.0027979 | 18.58649 | 0.0010550 | 0.8672009 |
| 672.30 | 18.11787 | 657.6277 | 14.6723064 | 0.0039268 | 18.58930 | 0.0012339 | 0.7911967 |
| 672.35 | 19.18341 | 655.1985 | 17.1515175 | 0.0025202 | 18.58422 | 0.0010791 | 0.9242345 |
| 672.45 | 22.00000 | 648.7772 | 23.6728422 | 0.0060937 | 18.56686 | 0.0050064 | 1.2779368 |
| 672.55 | 21.58416 | 649.7252 | 22.8248386 | 0.0049004 | 18.56946 | 0.0037338 | 1.2314197 |
| 672.70 | 20.38889 | 652.4502 | 20.2497577 | 0.0027545 | 18.57671 | 0.0016448 | 1.0913159 |
| 673.05 | 16.29310 | 661.7878 | 11.2621850 | 0.0098528 | 18.59498 | 0.0018460 | 0.6091222 |
| 673.25 | 18.27778 | 657.2631 | 15.9868875 | 0.0036192 | 18.58669 | 0.0013493 | 0.8619517 |
| 673.30 | 19.37472 | 654.7623 | 18.5376731 | 0.0024280 | 18.58102 | 0.0012143 | 0.9988834 |
| 673.55 | 18.90909 | 655.8239 | 17.7261356 | 0.0027376 | 18.58291 | 0.0012526 | 0.9553027 |
| 673.55 | 16.40693 | 661.5283 | 12.0216795 | 0.0093532 | 18.59383 | 0.0019948 | 0.6500360 |
| 673.90 | 15.59140 | 663.3876 | 10.5124688 | 0.0133138 | 18.59601 | 0.0021887 | 0.5695697 |
| 674.25 | 18.70694 | 656.2847 | 17.9652882 | 0.0029620 | 18.58236 | 0.0013927 | 0.9683002 |
| 675.40 | 18.32985 | 657.1444 | 18.2556230 | 0.0035263 | 18.58166 | 0.0017140 | 0.9842273 |
| 675.70 | 17.90235 | 658.1190 | 17.5809889 | 0.0043954 | 18.58321 | 0.0019849 | 0.9482690 |
| 676.15 | 18.91157 | 655.8182 | 20.3318165 | 0.0027352 | 18.57650 | 0.0016465 | 1.0957276 |
| 676.55 | 20.32497 | 652.5959 | 23.9540624 | 0.0026934 | 18.56611 | 0.0022503 | 1.2909116 |
| 676.60 | 20.02457 | 653.2808 | 23.3192006 | 0.0024794 | 18.56806 | 0.0019623 | 1.2565634 |
| 676.85 | 24.00000 | 644.2176 | 32.6324221 | 0.0150551 | 18.53342 | 0.0239327 | 1.7695996 |
| 676.95 | 17.60784 | 658.7904 | 18.1595061 | 0.0051360 | 18.58186 | 0.0024782 | 0.9798370 |
| 677.25 | 19.34853 | 654.8220 | 22.4279950 | 0.0024378 | 18.57070 | 0.0017845 | 1.2085152 |
| 677.95 | 19.67846 | 654.0698 | 23.8801872 | 0.0023819 | 18.56635 | 0.0019765 | 1.2867295 |
| 678.05 | 18.72861 | 656.2353 | 21.8147260 | 0.0029354 | 18.57245 | 0.0020349 | 1.1757630 |
| 678.40 | 15.88235 | 662.7242 | 15.6757917 | 0.0117990 | 18.58720 | 0.0042998 | 0.8486693 |
| 678.80 | 20.05491 | 653.2116 | 25.5883913 | 0.0024955 | 18.56088 | 0.0023782 | 1.3788507 |
| 679.40 | 17.98825 | 657.9232 | 21.4768395 | 0.0042012 | 18.57335 | 0.0028301 | 1.1582872 |
| 679.50 | 16.96629 | 660.2531 | 19.2469438 | 0.0071496 | 18.57917 | 0.0038911 | 1.0395648 |
| 679.65 | 19.23937 | 655.0709 | 24.5791567 | 0.0024882 | 18.56416 | 0.0021879 | 1.3244624 |
| 679.75 | 19.19586 | 655.1701 | 24.5799238 | 0.0025127 | 18.56415 | 0.0022097 | 1.3245200 |
| 679.80 | 19.59906 | 654.2508 | 25.5492004 | 0.0023821 | 18.56101 | 0.0022627 | 1.3766606 |
| 680.05 | 20.54348 | 652.0978 | 27.9522879 | 0.0029248 | 18.55266 | 0.0033289 | 1.5065553 |
| 680.45 | 18.58848 | 656.5548 | 23.8952393 | 0.0031189 | 18.56628 | 0.0025952 | 1.2880163 |
| 681.30 | 15.60419 | 663.3584 | 17.9415882 | 0.0132448 | 18.58220 | 0.0063414 | 0.9720483 |
| 681.30 | 15.29304 | 664.0678 | 17.2322354 | 0.0149843 | 18.58379 | 0.0066415 | 0.9344406 |
| 681.60 | 17.65537 | 658.6821 | 22.9178750 | 0.0050087 | 18.56918 | 0.0038483 | 1.2365064 |
| 681.90 | 17.57976 | 658.8545 | 23.0455580 | 0.0052126 | 18.56879 | 0.0040514 | 1.2435229 |
| 682.15 | 22.33333 | 648.0172 | 34.1327919 | 0.0072168 | 18.52744 | 0.0123542 | 1.8436407 |
| 682.45 | 18.75000 | 656.1865 | 26.2634653 | 0.0029097 | 18.55859 | 0.0029236 | 1.4155214 |
| 682.55 | 18.10241 | 657.6629 | 24.8870583 | 0.0039584 | 18.56311 | 0.0035789 | 1.3420432 |
| 682.65 | 20.25641 | 652.7522 | 29.8978048 | 0.0026340 | 18.54538 | 0.0034278 | 1.6111786 |
| 683.35 | 18.80207 | 656.0678 | 27.2821484 | 0.0028496 | 18.55506 | 0.0030893 | 1.4703811 |
| 683.40 | 18.77230 | 656.1357 | 27.2643275 | 0.0028835 | 18.55512 | 0.0031221 | 1.4694456 |
| 684.30 | 20.40521 | 652.4130 | 31.8870645 | 0.0027710 | 18.53740 | 0.0041031 | 1.7184969 |
| 684.35 | 18.65079 | 656.4127 | 27.9372559 | 0.0030340 | 18.55271 | 0.0034503 | 1.5058276 |
| 684.80 | 20.70707 | 651.7248 | 33.0752493 | 0.0031397 | 18.53237 | 0.0050056 | 1.7828616 |
| 684.95 | 22.00000 | 648.7772 | 36.1728422 | 0.0060937 | 18.51819 | 0.0116893 | 1.9527273 |
| 686.05 | 17.69978 | 658.5809 | 27.4691918 | 0.0048924 | 18.55430 | 0.0053989 | 1.4819807 |
| 686.70 | 21.48329 | 649.9552 | 36.7447808 | 0.0046457 | 18.51560 | 0.0091689 | 1.9821590 |
| 687.55 | 16.70103 | 660.8578 | 26.6921837 | 0.0081426 | 18.55688 | 0.0085402 | 1.4424181 |
| 689.10 | 19.57567 | 654.3042 | 34.7958028 | 0.0023837 | 18.52485 | 0.0041997 | 1.8748943 |
| 691.05 | 17.25806 | 659.5879 | 31.4621134 | 0.0061658 | 18.53893 | 0.0089489 | 1.6984884 |
| 691.35 | 17.37526 | 659.3207 | 32.0292749 | 0.0058026 | 18.53661 | 0.0087217 | 1.7287909 |
| 691.90 | 17.34931 | 659.3798 | 32.5201770 | 0.0058814 | 18.53454 | 0.0091147 | 1.7553571 |
| 693.95 | 16.26229 | 661.8581 | 32.0919525 | 0.0099910 | 18.53606 | 0.0152039 | 1.7358342 |
| 694.25 | 17.70045 | 658.5793 | 35.6706910 | 0.0048906 | 18.52064 | 0.0091008 | 1.9244552 |
| 694.80 | 20.12881 | 653.0431 | 41.7569351 | 0.0025400 | 18.49022 | 0.0064467 | 2.2501556 |
| 695.20 | 18.26539 | 657.2914 | 37.9085959 | 0.0036418 | 18.51004 | 0.0076347 | 2.0439093 |
| 695.30 | 14.54214 | 665.7797 | 29.5203181 | 0.0197142 | 18.54585 | 0.0258910 | 1.6046353 |
| 696.55 | 19.15261 | 655.2687 | 41.2813773 | 0.0025396 | 18.49279 | 0.0062997 | 2.2245288 |
| 698.20 | 17.36574 | 659.3424 | 38.8575607 | 0.0058314 | 18.50509 | 0.0129014 | 2.0973803 |
| 698.25 | 15.13898 | 664.4190 | 33.8310304 | 0.0158934 | 18.52812 | 0.0272017 | 1.8353793 |
| 698.45 | 17.84266 | 658.2551 | 40.1948450 | 0.0045362 | 18.49833 | 0.0107106 | 2.1681499 |
| 699.10 | 15.40704 | 663.8079 | 35.2921243 | 0.0143320 | 18.52161 | 0.0266093 | 1.9131285 |
| 700.30 | 18.86534 | 655.9236 | 44.3764533 | 0.0027816 | 18.47552 | 0.0079772 | 2.3916032 |
| 704.30 | 16.47413 | 661.3751 | 42.9249647 | 0.0090664 | 18.48300 | 0.0246377 | 2.3207019 |
| 706.75 | 17.86263 | 658.2096 | 48.5404085 | 0.0044886 | 18.45005 | 0.0154546 | 2.6182552 |
| 645.00 | 21.88586 | 649.0374 | -4.0373950 | 0.0057432 | 18.60218 | 0.0001371 | -0.2179132 |
| 672.20 | 20.20000 | 652.8808 | 19.3191890 | 0.0025898 | 18.57910 | 0.0014071 | 1.0410789 |
| 655.75 | 19.03640 | 655.5336 | 0.2163941 | 0.0026242 | 18.60323 | 0.0000002 | 0.0116613 |
Calculating R2 in R II
- Or, simpler, can calculate R2 in
Ras the ratio of variances in model vs. actual
# as ratio of variances
school_reg %>%
augment() %>%
summarize(r_sq = var(.fitted)/var(testscr)) # var. of *predicted* testscr over var. of *actual* testscr| r_sq |
|---|
| 0.0512401 |
R2=var(ˆY)var(Y)=1n−1∑ni=1(^Yi−ˉY)21n−1∑ni=1(Yi−ˉY)2→SSMSST
- SSM and SST are simply the numerators of the variance of ˆY and Y, respectively (i.e. before dividing by n−1, which will cancel out).
Standard Error of the Regression
- Standard Error of the Regression1, ˆσu is an estimator of the standard deviation of ui
^σu=√SSRn−2=√∑ˆu2in−2
- Measures ≈ average residual (distance between data points & regression line)
- Degrees of Freedom correction of n−2: we use up 2 df to first calculate ^β0 and ^β1!
Calculating SER in R
| SSR | df | SER |
|---|---|---|
| 144315.5 | 418 | 18.58097 |
Goodness of Fit: Looking at R I
Call:
lm(formula = testscr ~ str, data = ca_school)
Residuals:
Min 1Q Median 3Q Max
-47.727 -14.251 0.483 12.822 48.540
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 698.9330 9.4675 73.825 < 2e-16 ***
str -2.2798 0.4798 -4.751 2.78e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 18.58 on 418 degrees of freedom
Multiple R-squared: 0.05124, Adjusted R-squared: 0.04897
F-statistic: 22.58 on 1 and 418 DF, p-value: 2.783e-06summary()command inBase Rgives:Multiple R-squaredResidual standard error(SER)- Calculated with a df of n−2
Goodness of Fit: Looking at R II
| r.squared | adj.r.squared | sigma | statistic | p.value | df | logLik | AIC | BIC | deviance | df.residual | nobs |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0512401 | 0.0489703 | 18.58097 | 22.57511 | 2.8e-06 | 1 | -1822.25 | 3650.499 | 3662.62 | 144315.5 | 418 | 420 |
Two Types of Uses For Regression
Y=β(X)
where Y is numeric:
- Causal inference: estimate ˆβ to determine how changes in X cause changes in Y
- Care more about accurately estimating and understanding β
- Remove as much bias in β as possible
- Don’t care much about goodness of fit! (You’ll never get it in the complex real world)
- Prediction: predict ˆY using an estimated β
- Care more about getting ˆY as accurate as possible, f is an unknown “black-box”
- Tweak models to maximize R2, minimize ˆσu (at all costs)
Two Types of Uses For Regression
Example
Supplemental Nutrition Assistance Program (SNAP aka “Food Stamps”) is a federal welfare program designed to assist those in poverty by supplementing their budget for nutritious food.
- Causal inference: what is the affect of SNAP on poverty reduction?
- Prediction: who will enroll in SNAP?
Two Types of Uses For Regression
Example
Netflix uses your past viewing history, the day of the week, and the time of the day to guess which show you want to watch next
- Causal inference: how does the time of day affect what shows people select?
- Prediction: what will be the next show you select?
The Sampling Distributions of the OLS Estimators
Recall: Two Big Problems with Data
- We use econometrics to identify causal relationships & make inferences about them:
- Problem for identification: endogeneity
- X is exogenous if its variation is unrelated to other factors (u) that affect Y
- X is endogenous if its variation is related to other factors (u) that affect Y
- Problem for inference: randomness
- Data is random due to natural sampling variation
- Taking one sample of a population will yield slightly different information than another sample of the same population


Distributions of the OLS Estimators
Yi=β0+β1Xi+ui
OLS estimators (^β0 and ^β1) are computed from a finite (specific) sample of data
Our OLS model contains 2 sources of randomness:
- Modeled randomness: population ui includes all factors affecting Y other than X
- different samples will have different values of those other factors (ui)
- Sampling randomness: different samples will generate different OLS estimators
- Thus, ^β0,^β1 are also random variables, with their own sampling distribution
Inferential Statistics and Sampling Distributions
Inferential statistics analyzes a sample to make inferences about a much larger (unobservable) population
Population: all possible individuals that match some well-defined criterion of interest
- Characteristics about (relationships between variables describing) populations are called “parameters”
Sample: some portion of the population of interest to represent the whole
- Samples examine part of a population to generate .hi-turquoise[statistics] used to estimate population parameters

Sampling Basics
Example
Suppose you randomly select 100 people and ask how many hours they spend on the internet each day. You take the mean of your sample, and it comes out to 5.4 hours.
- 5.4 hours is a sample statistic describing the sample; we are more interested in the corresponding parameter of the relevant population (e.g. all Americans)
- If we take another sample of 100 people, would we get the same number?
Roughly, but probably not exactly
Sampling variability describes the effect of a statistic varying somewhat from sample to sample
- This is normal, not the result of any error or bias!
i.i.d. Samples
If we collect many samples, and each sample is randomly drawn from the population (and then replaced), then the distribution of samples is said to be independently and identically distributed (i.i.d.)
Each sample is independent of each other sample (due to replacement)
Each sample comes from the identical underlying population distribution

The Sampling Distribution of OLS Estimators
Calculating OLS estimators for a sample makes the OLS estimators themselves random variables:
Draw of i is random ⟹ value of each (Xi,Yi) is random ⟹ ^β0,^β1 are random
Taking different samples will create different values of ^β0,^β1
Therefore, ^β0,^β1 each have a sampling distribution across different samples

The Central Limit Theorem
The Central Limit Theorem
If we collect samples of size n from the same population and generate a sample statistic (e.g. OLS estimator), then with large enough n, the distribution of the sample statistic is approximately normal if:
- n≥30
- Samples come from a known normal distribution ∼N(μ,σ)
If neither of these are true, we have other methods (coming shortly!)
One of the most fundamental principles in all of statistics
Allows for virtually all testing of statistical hypotheses → estimating probabilities of values on a normal distribution
The Sampling Distribution of ^β1 I
The CLT allows us to approximate the sampling distributions of ^β0 and ^β1 as normal
We care about ^β1 (slope) since it has economic meaning, rarely about ^β0 (intercept)
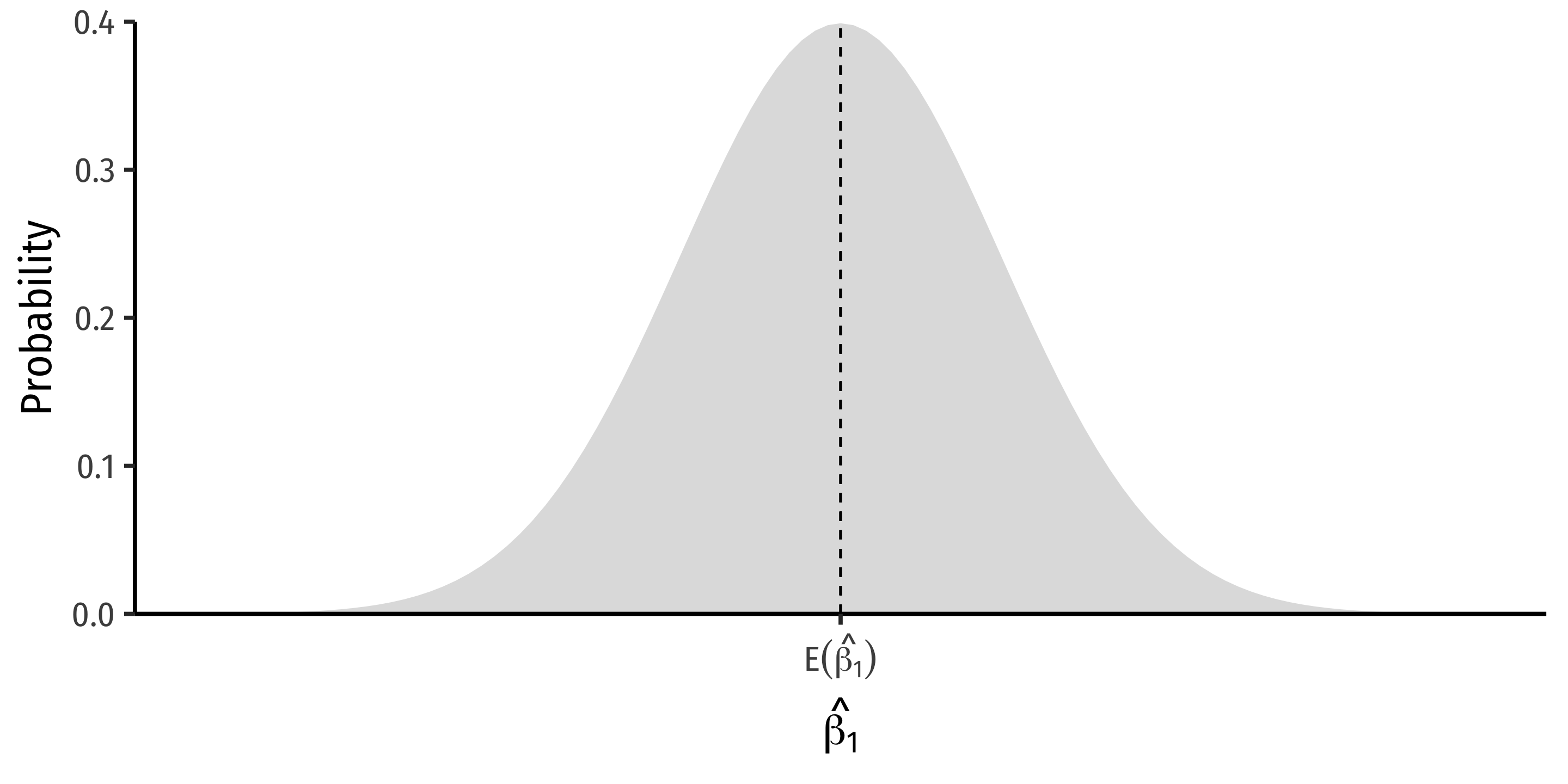
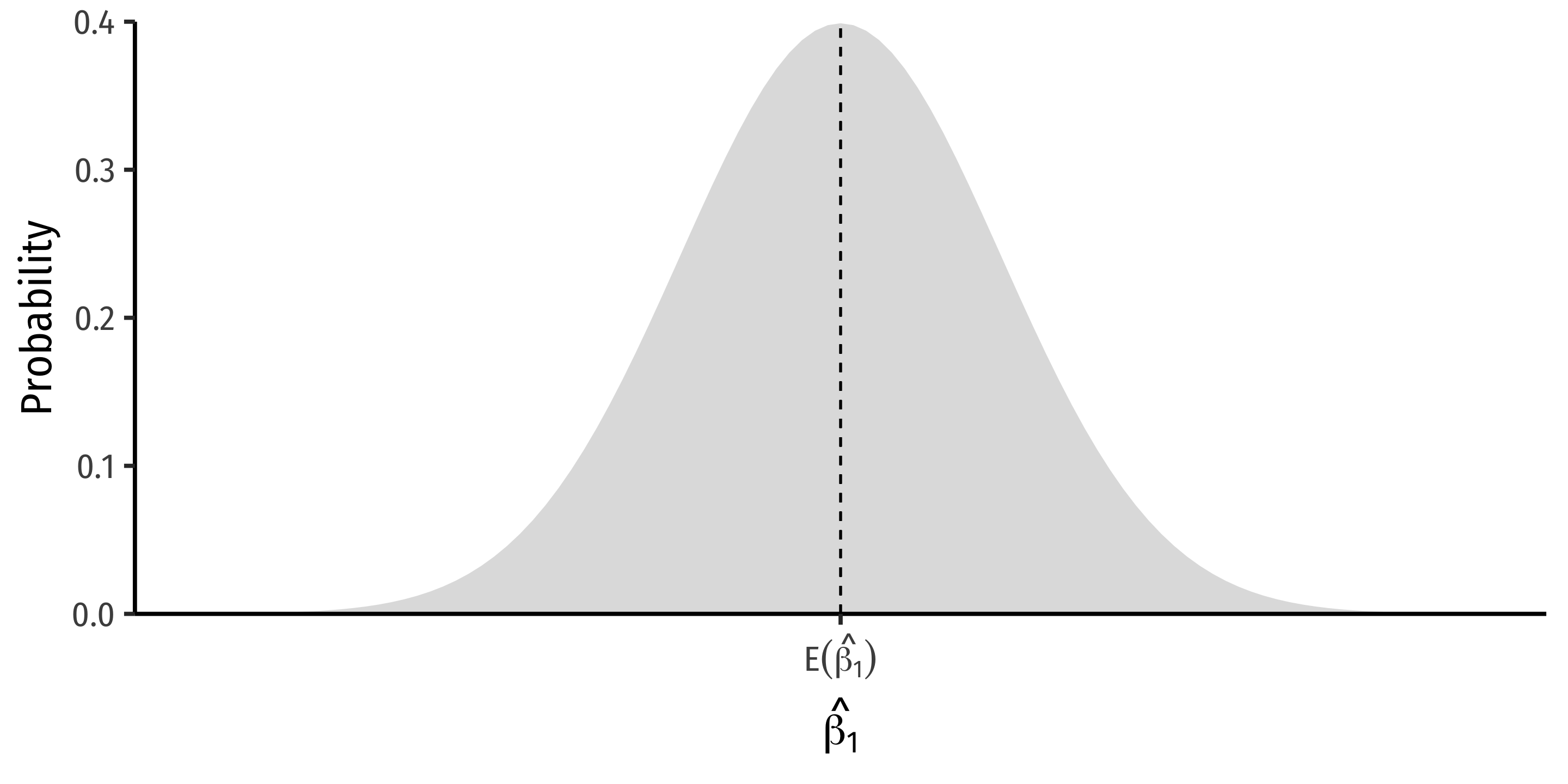
^β1∼N(E[^β1],σ^β1)
The Sampling Distribution of ^β1 II
^β1∼N(E[^β1],σ^β1)
- We want to know:
E[^β1]; what is the center of the distribution? (today)
σ^β1; how precise is our estimate? (next class)
Bias and Exogeneity
Assumptions about Errors I
In order to talk about E[^β1], we need to talk about population u
Recall: u is a random variable, and we can never measure the error term

Assumptions about Errors II
- We make 4 critical assumptions about u:
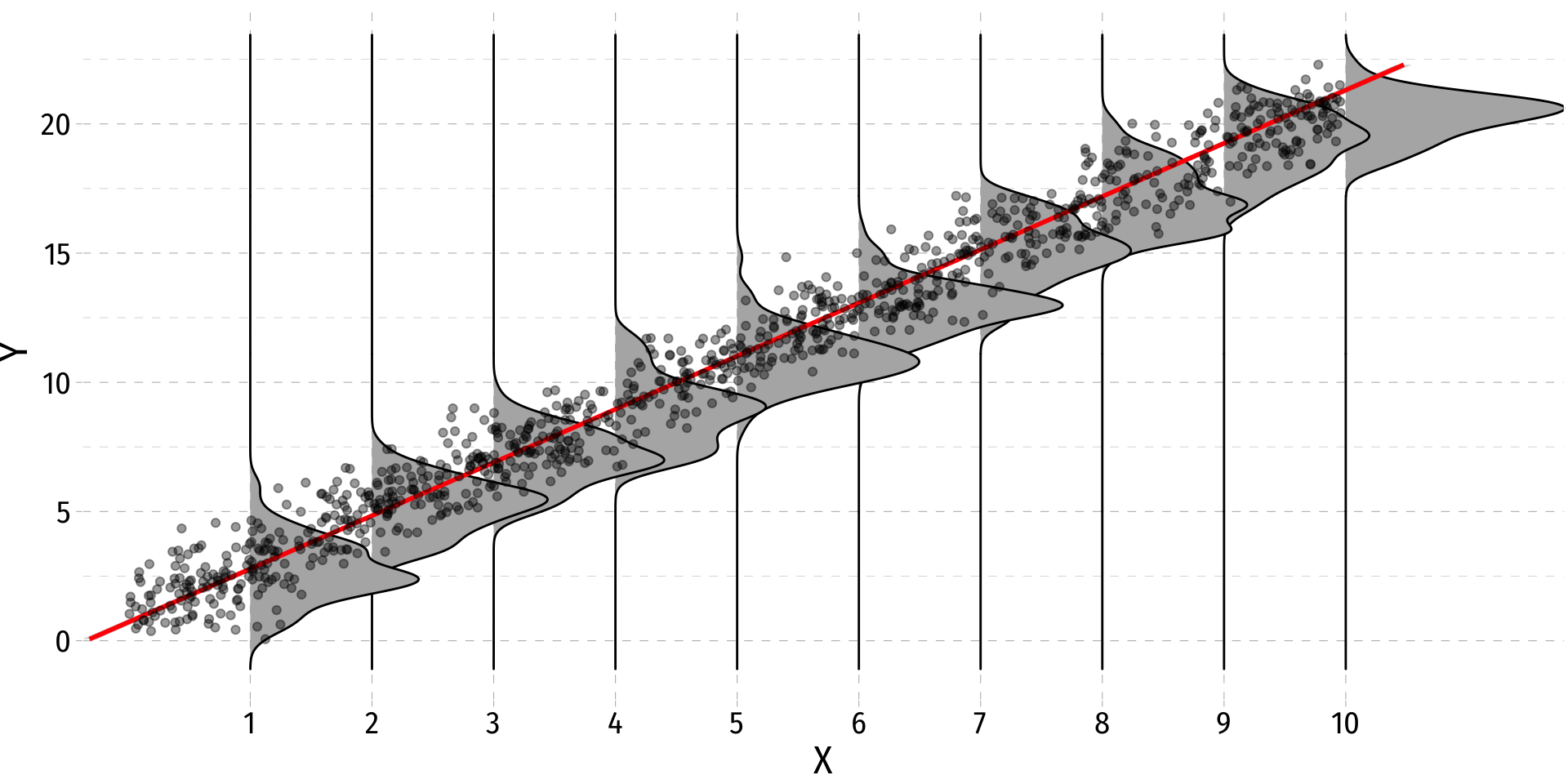
- The expected value of the errors is 0
E[u]=0

Assumptions about Errors II
- We make 4 critical assumptions about u:
- The expected value of the errors is 0
E[u]=0
- The variance of the errors over X is constant:
var(u|X)=σ2u

Assumptions about Errors II
- We make 4 critical assumptions about u:
- The expected value of the errors is 0
E[u]=0
- The variance of the errors over X is constant:
var(u|X)=σ2u
- Errors are not correlated across observations:
cor(ui,uj)=0∀i≠j

Assumptions about Errors II
- We make 4 critical assumptions about u:
- The expected value of the errors is 0
E[u]=0
- The variance of the errors over X is constant:
var(u|X)=σ2u
- Errors are not correlated across observations:
cor(ui,uj)=0∀i≠j
- There is no correlation between X and the error term:
cor(X,u)=0 or E[u|X]=0

Assumptions about Errors III
- The expected value of the errors is 0
E[u]=0
- The variance of the errors over X is constant:
var(u|X)=σ2u
- The first two assumptions ⟹ errors are i.i.d., drawn from the same distribution with mean 0 and variance σ2u
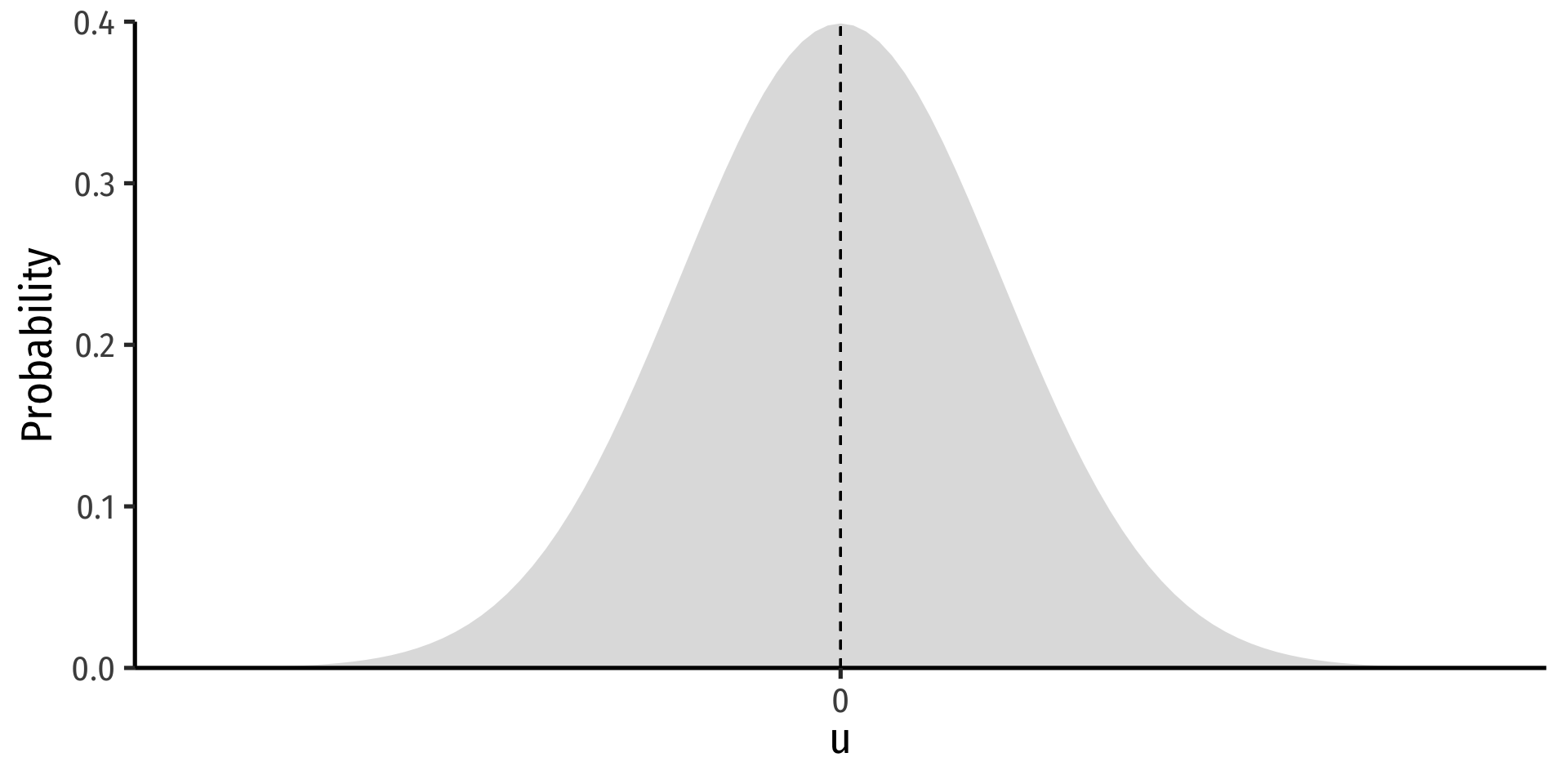
Assumptions about Errors: Homoskedasticity
- The variance of the errors over X is constant:
var(u|X)=σ2u
Assumption 2 implies that errors are “homoskedastic”: they have the same variance across X
Often this assumption is violated: errors may be “heteroskedastic”: they do not have the same variance across X
This is a problem for inference, but we have a simple fix for this (next class)
Assumption 3: No Serial Correlation
- Errors are not correlated across observations:
cor(ui,uj)=0∀i≠j
For simple cross-sectional data, this is rarely an issue
Time-series & panel data nearly always contain serial correlation or autocorrelation between errors
e.g. “this week’s sales look a lot like last week’s sales, which look like…etc”
There are fixes to deal with autocorrelation (coming much later)

Assumption 4: The Zero Conditional Mean Assumption
- No correlation between X and the error term:
cor(X,u)=0
This is the absolute killer assumption, because it assumes exogeneity
Often called the Zero Conditional Mean assumption:
E[u|X]=0
“Does knowing Xi give any useful information about ui?”
- If yes: model is endogenous, biased and not-causal!

Exogeneity and Unbiasedness
- ^β1 is unbiased iff there is no systematic difference, on average, between sample values of ^β1 and true population parameter β1, i.e.
E[^β1]=β1
Does not mean any sample gives us ^β1=β1, only the estimation procedure will, on average, yield the correct value
Random errors above and below the true value cancel out (so that on average, E[ˆu|X]=0)
Sidenote: Statistical Estimators I
- In statistics, an estimator is a rule for calculating a statistic (about a population parameter)
Example
We want to estimate the average height (H) of U.S. adults (population) and have a random sample of 100 adults.
Calculate the mean height of our sample (ˉH) to estimate the true mean height of the population (μH)
ˉH is an estimator of μH
- There are many estimators we could use to estimate μH
- How about using the first value in our sample: H1 ?
Sidenote: Statistical Estimators II
- What makes one estimator (e.g. ˉH) better than another (e.g. H1)?1
Unbiasedness: does the estimator give us the true parameter on average?
Efficiency: an estimator with a smaller variance is better
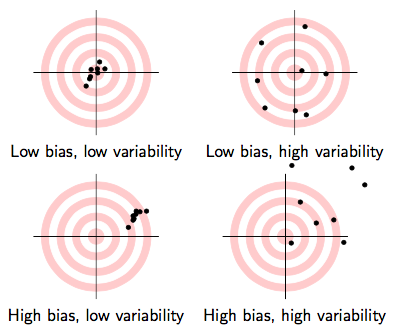
Exogeneity and Unbiasedness II
^β1 is the Best Linear Unbiased Estimator (BLUE) estimator of β1 when X is exogenous1
No systematic difference, on average, between sample values of ^β1 and the true population β1:
E[^β1]=β1
- Does not mean that each sample gives us ^β1=β1, only the estimation procedure will, on average, yield the correct value

Exogeneity and Unbiasedness III
- Recall, an exogenous variable (X) is unrelated to other factors affecting Y, i.e.:
cor(X,u)=0
- Again, this is called the Zero Conditional Mean Assumption
E(u|X)=0
For any known value of X, the expected value of u is 0
Knowing the value of X must tell us nothing about the value of u (anything else relevant to Y other than X)
We can then confidently assert causation: X→Y
Endogeneity and Bias
- Nearly all independent variables are endogenous, they are related to the error term u
cor(X,u)≠0
Example
Suppose we estimate the following relationship:
Violent crimest=β0+β1Ice cream salest+ut
We find ^β1>0
Does this mean Ice cream sales → Violent crimes?
Endogeneity and Bias: Takeaways
- The true expected value of ^β1 is actually:1
E[^β1]=β1+cor(X,u)σuσX
- If X is exogenous: cor(X,u)=0, we’re just left with β1
- The larger cor(X,u) is, larger bias: (E[^β1]−β1)
- We can “sign” the direction of the bias based on cor(X,u)
- Positive cor(X,u) overestimates the true β1 (^β1 is too high)
- Negative cor(X,u) underestimates the true β1 (^β1 is too low)
Endogeneity and Bias: Example I
Example
wagesi=β0+β1educationi+u
Is this an accurate reflection of education→wages?
Does E[u|education]=0?
What would E[u|education]>0 mean?
Endogeneity and Bias: Example II
Example
per capita cigarette consumption=β0+β1State cig tax rate+u
Is this an accurate reflection of taxes→consumption?
Does E[u|tax]=0?
What would E[u|tax]>0 mean?

